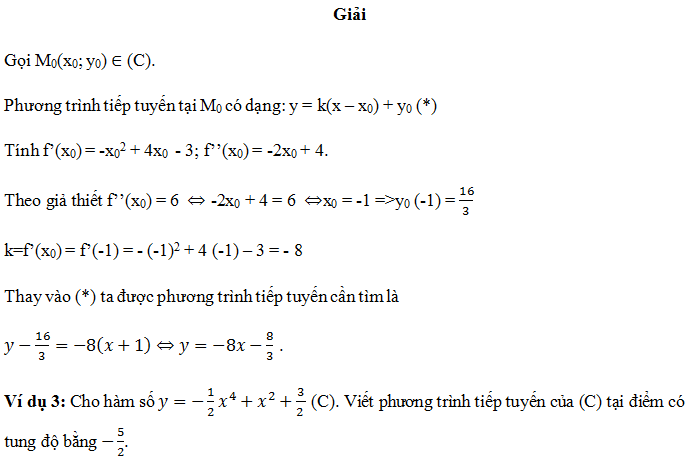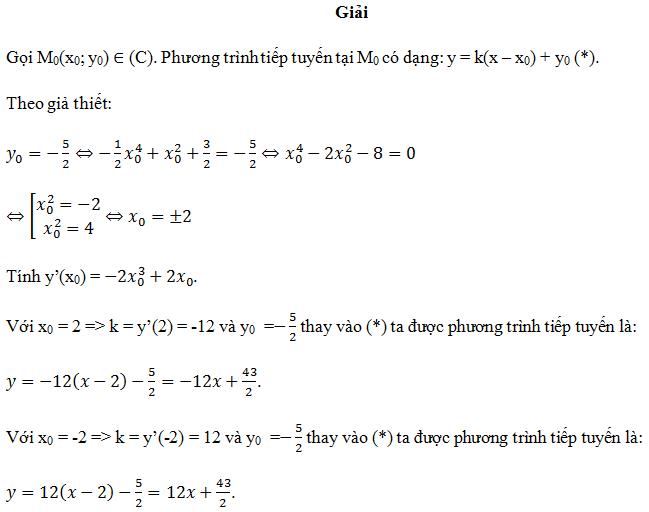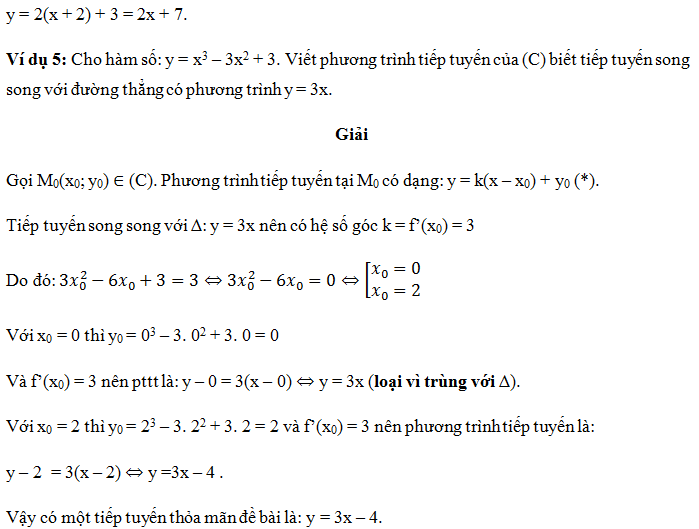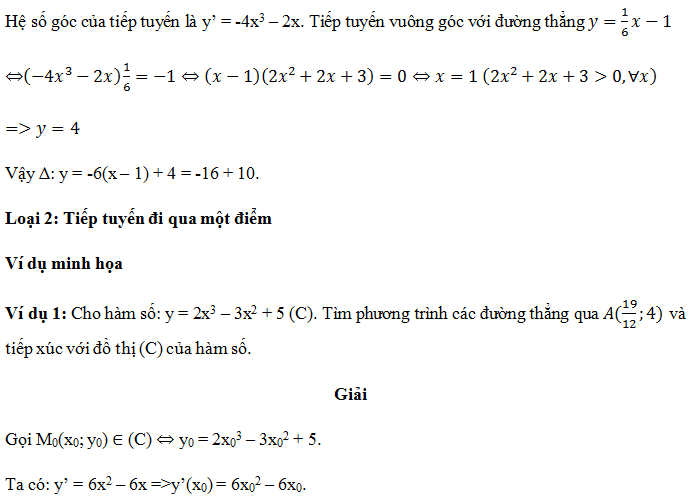Bạn đang xem: Viết phương trình tiếp tuyến của đồ thị hàm số Tại DongnaiArt

Phương trình tiếp tuyến của đồ thị hàm số có nhiều dạng như: viết pttt của hàm số tại một điểm, đi qua một điểm, biết hệ số góc … nhưng phần này không khó. phương pháp của từng loại này.

i.theory: vấn đề tiếp tuyến với đường cong:

phương pháp 1: sử dụng tọa độ liên hệ

Phương trình tiếp tuyến có dạng: y = f ‘(x0). (x – x0) + y0

1. lập phương trình cho tiếp tuyến của đường cong tại điểm m (x0, y0) của đồ thị hàm số (nghĩa là, tiếp tuyến duy nhất nhận m (x0; y0) làm tiếp tuyến).

phương trình tiếp tuyến của hàm số (c): y = f (x) tại điểm m (x0; y0) ∈ (c)

(hoặc trong h x = x0) có dạng: y = f ‘(x0). (x – x0) + y0.

2. Lập phương trình của tiếp tuyến d với đường cong đi qua điểm a (xa, ya) đã cho, bao gồm điểm trên đồ thị của hàm số (tức là bất kỳ tiếp tuyến nào qua a (xa, ya)).

cho hàm (c): y = f (x). Giả sử tiếp tuyến là m (x0, y0) thì phương trình của tiếp tuyến có dạng: y = f ‘(x). (x – x0) + y0 (d).

điểm a (xa, ya) ∈ d, ta được: ya = f ‘(x0). (xa – x0) + y0 = & gt; x0

từ đó lập phương trình của tiếp tuyến d.

.

3. tiếp tuyến của hình lập phương d với một đường cong có độ dốc k

cho hàm (c): y = f (x). giả sử tiếp điểm là m (x0; y0) thì phương trình tiếp tuyến có dạng: d: y = f ‘(x0). (x – x0) + y0.

Tiếp tuyến nằm ngang của tiếp tuyến d là nghiệm của phương trình:

f ‘(x0) = k = & gt; x0, thay vì hàm chúng ta nhận được y0 = f (x0).

chúng ta có thể thiết lập phương trình tiếp tuyến d: y = f ‘(x0). (x – x0) + y0.

phương pháp 2: sử dụng điều kiện phơi sáng

phương trình của đường thẳng đi qua điểm m (x0; y0) có hệ số góc k có dạng;

d: y = g ‘(x) = k. (x – x0) + y0.

Điều kiện để đường thẳng y = g (x) tiếp xúc với đồ thị của hàm số y = f (x) là hệ phương trình sau có nghiệm: ( left { begin {matrix} f (x) = g (x) & \ f ‘(x) = g’ (x) & end {matrix} right. ) nơi xuất phát của tiếp tuyến d.

ii. bài tập

Xem Thêm : Thẻ Debit Card là gì? Khác gì với thẻ Credit Card. Nên làm thẻ nào?

loại 1: cho hàm y = f (x). Viết phương trình của tiếp tuyến tại điểm m0 (x0; y0) ∈ (c).

người chiến thắng

phương trình của tiếp tuyến tại m0 có dạng: y = k (x – x0) + y0 (*)

trong đó x0 là tọa độ tiếp xúc;

trong đó y0 = f (x0) là tiếp tuyến của tiếp điểm;

trong đó k = y ‘(x0) = f’ (x0) là hệ số góc của tiếp tuyến.

Để viết một phương trình tiếp tuyến, chúng ta phải xác định x0; y0 và k.

một số hình dạng cơ bản

dạng 1: viết phương trình của tiếp tuyến tại m0 (x0; y0) ∈ (c)

– Tính đạo hàm của hàm số, thay x0 để được hệ số góc

áp dụng (*), chúng tôi nhận được phương trình tiếp tuyến bắt buộc.

dạng 2: đã cho tọa độ liên hệ x0

– Tính đạo hàm của hàm số, nhập x0 để có hệ số góc.

– thay x0 trong hàm chúng tôi tìm tọa độ tiếp điểm.

áp dụng (*), chúng tôi nhận được phương trình tiếp tuyến bắt buộc.

dạng 3: cho trước tọa độ tiếp xúc y0

-giải phương trình y0 = f (x0) để tìm x0.

– Tính đạo hàm của hàm số, nhập x0 để có hệ số góc.

áp dụng (*), chúng tôi nhận được phương trình tiếp tuyến bắt buộc.

lưu ý: có bao nhiêu giá trị của x0 thì có bấy nhiêu tiếp tuyến.

dạng 4: cho trước hệ số góc của tiếp tuyến k = y ‘(x0) = f’ (x0)

– Tính đạo hàm và giải phương trình k = y ‘(x0) = f’ (x0) để tìm x0

Xem Thêm : dừng cấp chứng chỉ nghiệp vụ sư phạm

– thay x0 trong hàm tìm tọa độ tiếp điểm cần tìm.

lưu ý: có bao nhiêu giá trị của x0 thì có bấy nhiêu tiếp tuyến.

lưu ý: một số hình dạng khác

-Khi giả thiết yêu cầu viết phương trình của một tiếp tuyến biết tiếp tuyến đó vuông góc với đường thẳng: y = ax + b, điều này

& lt; = & gt; y ‘(x0). a = -1 ⇔ y ‘(x0) = -1 / a

… trở về 4.

– khi giả thuyết yêu cầu viết phương trình của một tiếp tuyến mà bạn biết tiếp tuyến đó song song với đường thẳng

y = ax + b nên ⇔ y ‘(x0) = a … này trở về dạng 4.

– khi giả thiết yêu cầu viết phương trình của đường tiếp tuyến tại giao điểm với đường thẳng y = ax + b, việc đầu tiên cần làm là tìm tọa độ giao điểm của (c) và đường thẳng… quay lại dạng 1.

chú ý:

cho hai đường thẳng d1: y = a1x + b1 trong đó a1 là hệ số góc của đường thẳng d1 và y = a2x + b2 trong đó a2 là hệ số góc của đường thẳng d2.

tất cả nội dung của bài viết. xem thêm và tải xuống tệp chi tiết bên dưới:

tải xuống

Trắc nghiệm Luyện tập môn Toán lớp 12: Xem ngay