Cùng xem Công thức phép tịnh tiến đầy đủ, chi tiết nhất – Lớp 11 – VietJack.com trên youtube.

Dịch Công thức – Toán lớp 11

1. Lý thuyết

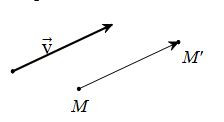
Trong mặt phẳng của vectơ. Phép biến hình biến mỗi điểm m thành điểm m’ sao cho mm’→=v→ được gọi là phép tịnh tiến theo véc tơ v→.

Phép tịnh tiến dọc theo vectơ v→ thường được biểu thị là tv→, và v→ được gọi là vectơ tịnh tiến.

Vậy, tv→m=m’⇔mm’→=v→.

Dịch chuyển theo vectơ – không được gọi là đồng nhất hóa. (Tự đưa ra từng điểm)

* thuộc tính

– Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kỳ.

– Làm cho một đường thẳng song song hoặc trùng với nó.

– Sử dụng công cụ này để biến một vectơ thành một vectơ.

– Sử dụng công cụ này để biến hình tam giác thành hình tam giác.

– Biến góc thành góc đều.

– Biến hình tròn thành hình tròn có cùng bán kính.

2. công thức

Trong mặt phẳng tọa độ Oxy của vectơ v→=a;b. Với mỗi điểm m(x;y) ta có m'(x’;y’) là ảnh của m tịnh tiến dọc theo v→. Khi đó mm’→=v→⇔x’=x+ay’=y+b.

(Tọa độ ảnh=tọa độ điểm+tọa độ vectơ tịnh tiến)

3. Ví dụ

Ví dụ 1: Trong mặt phẳng tọa độ Oxy của vectơ v→=(1;−5), điểm a(2; 2), đường thẳng d: 3x + 4y – 4 = 0, đường tròn : (c): x2 + y2 – 2x + 4y – 1 = 0 . định nghĩa:

a) Điểm a’ là ảnh của a qua phép tịnh tiến theo vectơ v→.

b) Đường thẳng d’ là ảnh của d sau phép tịnh tiến theo véc tơ v→.

c) Đường tròn (c’) là ảnh của (c) sau phép tịnh tiến theo véc tơ v→.

Giải pháp

a) Ta có a’, là hình ảnh qua tv→. Tọa độ a’: xa’=xa+1=3ya’=ya−5=−3. Vậy a'(3; -3).

b) Lấy điểm m(0; 1) thuộc d

Gọi m’ là hình ảnh của m qua tv→, sau đó gọi m’∈d’

Xem Thêm : TÌM HIỂU VỀ GIAO THỨC SPANNING TREE PROTOCOL –

Ta có: xm’=xm+1=1ym’=ym−5=−4. Vậy m'(1;-4) .

Vì d’ là ảnh của d qua tv→ nên d’ song song hoặc trùng với d. Suy ra vtpt nd’→=nd→=3;4.

Vậy phương trình d’: 3(x – 1) + 4(y + 4) = 0. hay d’: 3x + 4y + 13 = 0.

c) Cách 1: (tâm thuần i, giữ nguyên bán kính)

Phương trình đường tròn (c): x2 + y2 – 2x + 4y – 1 = 0

Tâm tại i (1; -2) và bán kính r=12+−22−−1=6

Qua TV → Hãy gọi tôi là hình ảnh của tôi. Ta có: xi’=xi+1=1+1=2yi’=yi−5=−2−5=−7.

Tôi'(1; -7)

Đường tròn (c’) là hình của (c) đi qua , nên tâm của (c’) là i’ và bán kính là .

Vậy phương trình (c’): (x-2)2 + (y+7)2 = 6 hoặc x2 + y2 – 4x + 7y + 47 = 0.

Cách 2: (biến đổi từng điểm trên đường tròn)

Với mọi điểm b(x;y) ∈(c). Gọi b'(x’;y’) là ảnh tịnh tiến của b.

Sau đó x’=x+1y’=y−5⇔x=x’−1y=y’+5

Vì bx;y∈c nên thay vào phương trình (c):

(x’- 1)2 + (y’ + 5)2 – 2(x’ – 1) + 4(y’+ 5) – 1 = 0

Suy ra x’2 + y’2 – 4x’ + 14y’ + 47 = 0

b'(x’;y’) b qua ảnh của tv → nên b’ di chuyển trên đường tròn (c’): x’2 + y’2 – 4x’ + 14y’ + 47 = 0

Vậy ảnh của (c) là đường tròn (c’): x’2 + y’2 – 4x’ + 14y’ + 47 = 0

Ví dụ 2: Cho hai parabol (p): y = x2 và (q): y = x2 + 2x + 2 trên mặt phẳng với hệ tọa độ Oxy. Tìm phép tịnh tiến để biến ( q ) thành (p).

Giải pháp

Gọi vectơ tịnh tiến là v→=a;b. Cho ảnh của (q) qua tv → gọi là parabol (r)

Lấy mx;y∈(q). Gọi m’x’;y’=tv→(m) thì m’∈r

Biểu thức tọa độ để áp dụng bản dịch: x’=x+ay’=y+b⇔x=x’−ay=y’−b

Vì , thế vào phương trình (q): y’ – b = (x’ – a)2 + 2(x’- a) + 2

⇔y’=x’2+ 21-ax’+a2-2a+b+2

Vậy phương trình (r): y = x2 + 2(1 – a)x + a2 – 2a + b + 2

Xem Thêm : Fax là gì? Số fax có bao nhiêu số, hướng dẫn cách gửi fax

Nếu (r) trùng với (p) thì 2(1−a)=0a2−2a+b+2=0

⇔a=112−2.1+b+2=0⇔a=1b=−1

Vậy theo vectơ v→−1;1 chỉ có một phép tịnh tiến biến parabol (q) thành parabol (p).

4. Bài tập tự rèn luyện

câu 1. Trên mặt phẳng tọa độ Oxy, cho phân số m(0; 1). Điểm m qua u→1;2 phép tịnh tiến theo véc tơ như thế nào?

a. m'(2; 3)

b. m'(1; 3)

c. m'(1; 1)

d. m'(-1; -1)

Câu 2. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x – 2y + 2 = 0. Hình dịch chuyển bởi đường thẳng d qua u→=2;3 có phương trình:

a. x + 2y + 2 = 0

b. x – 2y + 6 = 0

c. 2x – y + 2 = 0

d.2x + y +2 = 0

Câu 3. Trong mặt phẳng tọa độ Oxy, cho đường tròn (c): x2 + y2 – 2x + 4y – 4 = 0. Đường tròn (c) tịnh tiến ảnh của u→1 theo vectơ; 1 ​​là một đường tròn có phương trình:

a. (x – 2)2 + (y + 1)2 = 16

b. (x + 2)2 + (y – 1)2 = 9

c. (x – 2)2 + (y + 1)2 = 9

d. (x + 2)2 + (y + 1)2 = 9

Đáp án:1b, 2b, 3c

Xem tổng hợp công thức toán lớp 9 đầy đủ và chi tiết hơn:

Công thức đối xứng

Công thức đối xứng trục

công thức xoay

Công thức vị ngữ

Công thức đồng dạng

Nguồn: https://dongnaiart.edu.vn
Danh mục: Tin tức

Lời kết: Trên đây là bài viết Công thức phép tịnh tiến đầy đủ, chi tiết nhất – Lớp 11 – VietJack.com. Hy vọng với bài viết này bạn có thể giúp ích cho bạn trong cuộc sống, hãy cùng đọc và theo dõi những bài viết hay của chúng tôi hàng ngày trên website: Dongnaiart.edu.vn