Bạn đang xem: Lý Thuyết Và Bài Tập Các Tập Hợp Số Lớp 10 Tại DongnaiArt

Bộ là một khái niệm quen thuộc mà chúng ta học ở lớp sáu. Trong số đó, ngay từ bài học đầu tiên chúng ta đã được làm quen với tập hợp số tự nhiên và tìm hiểu về các tập hợp số khác như số nguyên, hợp số, số hữu tỉ, số vô tỉ, số thực trong chương trình toán thcs. Hôm nay, chúng tôi muốn giới thiệu với bạn đọc Bộ Số Lớp 10 trong Chương 1: Đặt Mệnh đề cho Chương trình Đại số Mười.

Tài liệu sẽ bao gồm lý thuyết và bài tập về các tập hợp số, quan hệ giữa các tập hợp, biểu diễn khoảng, đoạn, bán khoảng, tập con chung của số thực. Hi vọng đây sẽ là bài viết hữu ích giúp các bạn học tốt chương Tập hợp mệnh đề hơn.

i / Lý thuyết bộ số 10 lớp

Trong phần này, chúng tôi sẽ xem xét các định nghĩa của tập hợp số 10 hạng , các phần tử của mỗi tập hợp sẽ có dạng gì và cuối cùng xem xét mối quan hệ giữa chúng.

1. Tập hợp các số tự nhiên được biểu diễn bằng n

n = {0, 1, 2, 3, 4, 5, ..}.

2. Tập hợp các số nguyên thường được biểu diễn dưới dạng z

z = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4,…}.

Một tập hợp các số nguyên bao gồm các số tự nhiên và các phần tử tương hỗ của chúng.

Tập hợp các số nguyên dương được biểu diễn bởi n *

3. Tập hợp các số hữu tỉ, thường được biểu diễn bằng q

q = {a / b; a, b∈z, b ≠ 0}

Số hữu tỉ có thể được biểu diễn bằng số thập phân vô hạn hữu hạn hoặc lặp lại.

4. Tập hợp các số thực thường được biểu diễn dưới dạng r

Mọi số được biểu diễn bằng phân số vô hạn tuần hoàn được gọi là số vô tỉ. Tập hợp các số vô tỉ thường được biểu diễn bằng i . Tập hợp các số thực có chứa số hữu tỉ và vô tỉ.

5. Mối quan hệ của các tập dữ liệu

Chúng tôi có: r = q ∪ i.

Tập n; z; q; r.

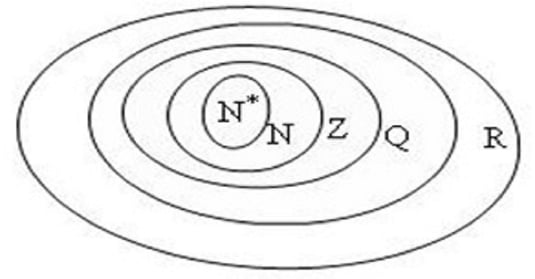
Mối quan hệ bao hàm giữa các tập hợp là: n ⊂ z ⊂ q ⊂ r

Mối quan hệ giữa các nhóm chữ số trong lớp 10 cũng được hiển thị bằng sơ đồ ven:

6. Tập hợp con thường xuyên của tập hợp các số thực

Ký hiệu -∞ được đọc là âm vô cùng (hoặc âm vô cùng) và ký hiệu + ∞ được đọc là dương vô cùng (hoặc dương vô cùng)

ii / Bài tập về mảng lớp 10

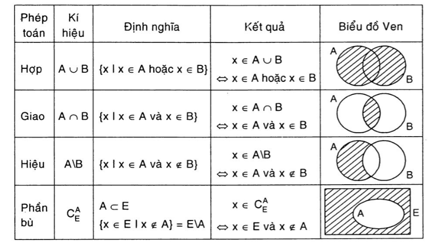
Sau khi ôn tập lý thuyết, chúng ta sẽ vận dụng những kiến ​​thức trên để giải các bài toán về Số 10 . Các dạng bài tập chính là liệt kê các phần tử trên tập hợp và các phép toán trên giao, hợp và hiệu của các tập hợp số thực.

Bài 1: Chọn câu trả lời đúng trong các câu sau:

a) [a; b] ⊂ (a; b] b) [a; b) ⊂ (a; b] c) [a; b] ⊂ (a; b) d) (a; b], [a; b) là tất cả các tập con của [a; b]

Người chiến thắng:

Chọn câu trả lời d. Vì [a; b] là tập hợp lớn nhất trong bốn tập hợp:

Bài tập 2: Xác định từng nhóm sau:

a) [-2; 4) ∪ (0; 5]

b) (-1; 6] ∩ [1; 7)

Xem Thêm : Học ngành Dược ra trường làm gì?

c) (-∞; 7) (1; 9)

Người chiến thắng:

a) [-2; 4) ∪ (0; 5] = [- 2; 5]

b) (-1; 6] ∩ [1; 7) = [1; 6]

c) (-∞; 7) (1; 9) = (- ∞; 1]

Đây là dạng toán thường gặp nhất, để giải nhanh bài toán này, trước tiên ta cần vẽ tập hợp trên trục số thực, phần lấy về giữ nguyên, phần không lấy sẽ gạch chéo. ra ngoài. Sau đó, sẽ dễ dàng hơn để nhận được giao hàng, công đoàn hoặc khác.

Bài tập 3: Xác định từng nhóm sau

a) (-∞; 1] ∩ (1; 2)

b) (-5; 7] ∩ [3; 8)

c) (-5; 2) ∪ [-1; 4]

d) (-3; 2) [0; 3]

e) r (-∞; 9)

Người chiến thắng:

a) (-∞; 1] ∩ (1; 2)

b) (-5; 7] ∩ [3; 8) = [3; 7)

c) (-5; 2) ∪ [-1; 4] = (-1; 2)

d) (-3; 2) [0; 3] = (-3; 0]

e) r (-∞; 9) = [9; + ∞)

Bài học 4 : Xác định các tập hợp sau bằng cách liệt kê

bài đăng 5: Liệt kê các phần tử của bộ sưu tập sau

Bài tập 6: Xác định các tập hợp sau và biểu diễn chúng trên trục số

a) [-3; 1) (0; 4]

b) [-3; 1) (0; 4]

c) (-∞; 1) (2; + ∞)

d) (-∞; 1) (2; + ∞)

Bản nhạc 7: a = (- 2; 3) và b = [1; 5]. Xác định tập hợp: a ∪ b, a ∩ b, ab, ba.

Xem Thêm : Thần số học số 7: Tri thức huyền bí của kẻ độc hành cô độc

Bài 8: Cho a = {x € r || x ≤ 4}; b = {x € r | -2 ≤ x + 1 <3}

Viết tập hợp sau dưới dạng khoảng-đoạn-bán-khoảng: a ∩ b, ab, ba, r (a∪b)

Điều 9 : Cho a = {x € r | -3 ≤ x ≤ 5} và b = {x € z | -1 <; x 5}

Xác định tập hợp: a ∪ b, a ∩ b, ab, ba

Đăng 10: for and a = {x € r | x> 2} and b = {x € r | -1 <x 5}

Xác định tập hợp: a ∪ b, a ∩ b, ab, ba

Bài 11 : Cho a = {2,7} và b = (- 3,5]. Xác định tập hợp: a ∪ b, a ∩ b, ab, ba

Bài 12: Xác định các tập hợp sau và biểu diễn chúng trên trục số

a) r ((0; 1) (2; 3))

b) r ((3; 5) (4; 6)

c) (-2; 7) [1; 3]

d) ((-1; 2) (3; 5)) (1; 4)

Bài 13: cho a = {x € r | 1 ≤ x ≤ 5}, b = {x € r | 4 x ≤ 7} và c = {x € r | 2≤ x <6}.

a) Xác định tập hợp: b) Gọi d = {x € r | a≤x≤b}. Xác định a, b là d⊂a∩b∩c

Bài tập 14: Viết phần bù vào r của tập hợp sau:

a = {x € r | -2 ≤ x <10}

b = {x € r || x | & gt; 2}

c = {x € r | -4 <x + 2 5}

bài đăng 15: cho a = {x € r | x ≤ -3 hoặc x> 6}, b = {x € r | x2- 25 0}

a) Tìm các nửa khoảng-đoạn-bán-đoạn sau: ab, ba, r (a ∪ b), r (a∩b), r (ab) b) cho c = {x € r | x≤ a}; d = {x € r | x ≥b}. Xác định a, b biết rằng c∩bvμd∩b lần lượt là các đoạn thẳng có độ dài 7 và 9. Tìm c∩d.

Đăng 16: Dành cho Bộ sưu tập

a = {x € r | -3 x ≤ 2}

b = {x € r | 0 x 7}

c = {x € r | x -1}

d = {x € r | x 5}

a) Viết lại tập hợp trên theo ký hiệu khoảng, khoảng và nửa khoảng b) Biểu diễn các tập a, b, c, d trên trục số

Chúng ta vừa xem xong Tập hợp số Bài 10 , chẳng hạn như số tự nhiên, số nguyên, số thực, số hữu tỉ, số vô tỉ và tập con của tập số. số thực. Nắm vững kiến ​​thức về tập hợp số sẽ giúp học sinh học đại số tốt hơn, vì rất nhiều môn toán liên quan đến tập hợp, chẳng hạn như tìm tập xác định của một hàm số, hoặc tìm tập nghiệm của một hàm số. Để học tốt phần thực hành tập hợp số, học sinh cần nắm được định nghĩa tập hợp số, dạng đặc trưng của từng phần tử của tập hợp và các phép toán giao, hợp, sai, bù của tập hợp. Để dễ nhớ các tập hợp, bạn có thể sử dụng sơ đồ ven để minh họa chúng một cách trực quan. Mình hi vọng bài viết này sẽ giúp các bạn nắm vững mảng và làm các bài tập liên quan đến mảng một cách chính xác.