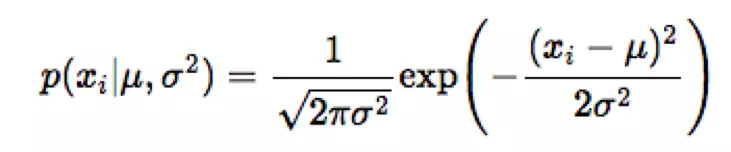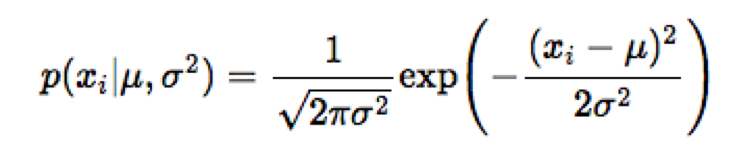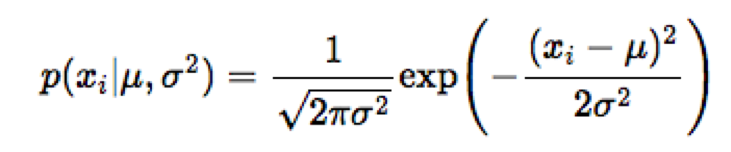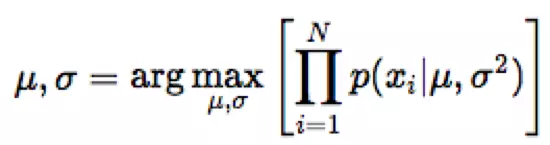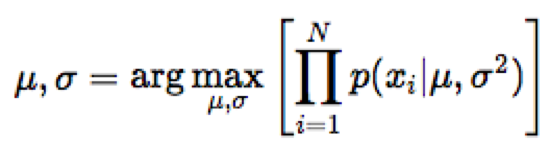Bạn đang xem: Sơ lược về Maximum Likelihood Estimation Tại DongnaiArt

đối với một vấn đề chung về máy học, việc giải quyết vấn đề thường bao gồm 3 bước chính:

• lập mô hình : tìm mô hình mô tả tốt nhất vấn đề
• tìm hiểu : tối ưu hóa các thông số mô hình dựa trên dữ liệu có sẵn
• suy luận : sử dụng mô hình được tối ưu hóa để dự đoán kết quả với thông tin không xác định

Trong học máy thống kê, các mô hình bài toán thường là sự kết hợp của các phân phối xác suất đơn giản (Bernoulli, Gaussian, v.v.). Trong bước tìm hiểu, có hai phương pháp thường được sử dụng để tối ưu hóa tập thông số, đó là ước tính khả năng xảy ra tối đa và ước tính hậu nghiệm tối đa.

Trong bài viết này, chúng ta sẽ tìm hiểu phương pháp ước tính khả năng xảy ra tối đa thông qua một ví dụ đơn giản. phương pháp ước tính tối đa sau sẽ được giới thiệu trong phần tiếp theo.

mle là một phương pháp dự đoán các tham số của mô hình thống kê dựa trên các “quan sát” có sẵn, bằng cách tìm một tập hợp các tham số sao cho có thể tối đa hóa xác suất mà mô hình với tập tham số đó có thể đạt được là cực đại. “quan sát” hiện có.

Giả sử mô hình được mô tả bởi tập tham số θ, các “quan sát” (hoặc điểm dữ liệu) là x1, x2, …, xn. vì vậy chúng tôi cần tìm:

θ = argmax {p (x1, x2,…, xn | θ)} (1)

Xem Thêm : Fall in love là gì? Các cụm từ về tình yêu phổ biến nhất

, trong đó: p (x1, x2,…, xn | θ) là xác suất để các sự kiện x1, x2,…, xn xảy ra đồng thời, được gọi là khả năng xảy ra. đó là lý do tại sao phương pháp này được gọi là khả năng tối đa.

Tuy nhiên, việc giải quyết vấn đề (1) một cách trực tiếp thường rất khó. chúng ta có thể đơn giản hóa vấn đề bằng cách giả định rằng các điểm dữ liệu xảy ra độc lập với nhau. vì vậy, (1) trở thành:

θ = argmax {∏ prod∏ p (xn | θ)} (2)

chúng tôi có thể làm cho việc tính toán dễ dàng hơn bằng cách chuyển đổi nó thành vấn đề có khả năng xảy ra tối đa trong nhật ký:

θ = argmax {∑ sum∑ log (p (xn | θ))} (3)

Để hiểu rõ hơn về mle, hãy làm một ví dụ đơn giản.

giả sử bài toán có 5 học sinh làm bài kiểm tra với số điểm lần lượt là 3, 6, 5, 9, 8. Để mô hình hóa điểm số của những sinh viên này, chúng tôi giả định rằng các điểm dữ liệu được phân phối theo phân phối Gauss:

Xem Thêm : Tìm hiểu về các PROSet/Phần mềm Vô tuyến

Để dự đoán tập hợp các tham số của phân phối chuẩn, chúng tôi sử dụng phương pháp mle:

Để tìm μ và σ sao cho biểu thức trong ngoặc đạt giá trị lớn nhất, chúng ta phân biệt biểu thức theo từng biến và giải phương trình khi giá trị đó bằng 0.

Từ đó ta có:

Thay các điểm dữ liệu vào công thức trên, chúng tôi tìm thấy μ = 6,2 và σ = 2,14.

Hy vọng rằng qua bài viết này, bạn sẽ hiểu rõ hơn về phương pháp ước tính khả năng xảy ra tối đa. Trong phần tiếp theo, chúng ta sẽ tìm hiểu về phương pháp ước tính tối đa sau tổng quát hơn.

• https://machinelearningcoban.com/2017/07/17/mlemap/
• https://towardsdatascience.com/probability-concept-explained-maximum-likel Name-estimation-c7b4342fdbb1