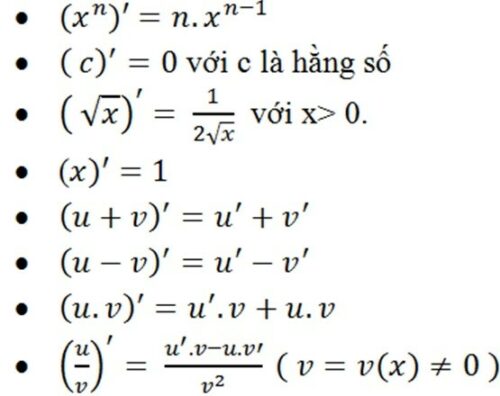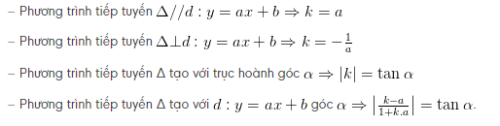Cùng xem Tổng hợp các công thức đạo hàm log, logarit, căn bậc 3 … – Marathon trên youtube.
Hàm số logarit và công thức tính Đạo hàm logarit là nội dung cần học trong môn Toán lớp 12. Đây là những kiến thức trọng tâm và thường xuyên xuất hiện trong các bài thi. Vì vậy, trong các bài viết tiếp theo, Marathon Education sẽ ôn tập các kiến thức cơ bản liên quan đến hàm số lôgarit, công thức tính đạo hàm lôgarit và các ví dụ minh họa để giúp các em nắm vững phần kiến thức này.
1. Tổ hợp các công thức đạo hàm
Quy tắc cơ bản cho công cụ phái sinh
2. Bảng đạo hàm lượng giác
3. Công thức đạo hàm logarit
4. Công thức đạo hàm theo cấp số nhân
5. Công thức đạo hàm logarit
6. Bảng đạo hàm và nguyên hàm
7. Câu hỏi về công thức đạo hàm
7.1 Tính đạo hàm theo định nghĩa
Hàm y = f(x) có đạo hàm x= x <=>> f'(x )=f'(x )
Đạo hàm của hàm số y = f(x) tại một điểm trước tiên phải liên tục tại điểm đó.
Ví dụ 1: f(x) = 2x +1 tại x=2
7.2 Chứng minh rằng các đạo hàm bằng nhau
Ví dụ 1: Cho y = e .sinx, chứng minh hệ thức y”+2y′+ 2y = 0
Giải pháp:
Ta có y′=−e .sinx + e .cosx
y′ =−e.sinx+e−x.cosx
y”=e .sinx−e .cosx−e .cosx−e .sinx = −2e .cosx
Vậy y”+ 2y′+ 2y = −2.e .cosx− −2.e .sinx + 2.e .cosx + 2.e .sinx =0
7.3 Viết phương trình tiếp tuyến cho các tiếp điểm đã biết
Phương trình tiếp tuyến của đường cong (c): y= f(x) tại tiếp điểm m( x ;y ) có dạng:
Ví dụ, đối với hàm y= x +3mx + ( m+1)x + 1 (1), m là tham số thực. tìm giá trị
m làm tiếp tuyến của đồ thị hàm số (1) tại tọa độ x = -1 đi qua điểm a(
1;2).
Xác định tập hợp d = r
y’ = f'(x)= 3x + 6mx + m + 1
x = -1 => y = 2m -1, f'( -1) = -5m + 4
Phương trình tiếp tuyến tại điểm m( -1; 2m – 1): y= ( -5m + 4 ) ( x+1) + 2m -1 (d)
Ta có ( 1;2) ∈ (d) (-5m + 4).2 + 2m – 1 = 2 => mét = 5/8
7.4 Viết phương trình khi biết hệ số góc
Viết pttt Δ của ( c ) : y = f( x ), giả sử Δ có hệ số góc k cho trước
Gọi m( x ;y ) liên hệ. Tính y’ => y'(x )
Xem Thêm : 8 các bước lập trình PLC căn bản nhất cho người mới!
Vì phương trình tiếp tuyến Δ có hệ số góc k =>;y’ = ( x ) = k (i)
Giải (i) tìm x => y = f(x ) => : y = k (x – x )+ y
Lưu ý: Hệ số góc của tiếp tuyến k = y'( x ) thường được tính gián tiếp như sau:
Ví dụ: Cho hàm số y=x +3x -9x+5 ( c). Trên tất cả các tiếp tuyến của đồ thị ( c ), hãy
Tìm tiếp tuyến có hệ số góc nhỏ nhất.
Ta có y’ = f'( x ) = 3x + 6x – 9
Gọi x là hoành độ của tiếp tuyến nên f'( x ) = 3 x + 6 x – 9
Ta có 3 x + 6 x – 9 = 3 ( x + 2x +1) – 12 = 3 (x +1) – 12 > – 12
Vậy f( x )= – 12 nhỏ nhất tại x = -1 => y = 16
Đạo hàm của phương trình tiếp tuyến: y= -12(x+1)+16 y= -12x + 4
7.5 Đạo hàm và bất đẳng thức
Đánh giá khóa học trực tuyến về giáo dục Marathon
Team Marathon Education vừa chia sẻ với các bạn những kiến thức quan trọng về hàm số logarit và công thức tính đạo hàm logarit. Hi vọng bài viết này sẽ cung cấp cho các em những kiến thức nền tảng cần thiết giúp các em học tốt môn Toán hơn và đạt điểm cao trong kì thi sắp tới. Để tìm hiểu thêm trực tuyến, đừng quên theo dõi Marathon mỗi ngày. chúc may mắn!
Nguồn: https://dongnaiart.edu.vn
Danh mục: Tin tức
Lời kết: Trên đây là bài viết Tổng hợp các công thức đạo hàm log, logarit, căn bậc 3 … – Marathon. Hy vọng với bài viết này bạn có thể giúp ích cho bạn trong cuộc sống, hãy cùng đọc và theo dõi những bài viết hay của chúng tôi hàng ngày trên website: Dongnaiart.edu.vn
