Bạn đang xem: Công thức, Điều kiện và Bài tập cực trị của hàm số bậc 4 Tại DongnaiArt

Giá trị cực trị của hàm số bậc hai là một trong những chuyên đề trọng tâm trong chương trình môn Toán lớp 12 và kỳ thi tuyển sinh THPT quốc gia. Vậy cực trị của hàm bậc hai là gì? Lý thuyết và bài tập về cực trị của hàm số bậc hai? Công thức giá trị cực trị của hàm số bậc hai? …Trong bài viết sau, dinhnghia.vnsẽ giúp bạn tổng hợp kiến ​​thức về các chủ đề trên, hãy cùng cùng tìm hiểu nhé!

Cực trị của hàm số là gì?

Cho hàm số \( y= f(x) \) liên tục và xác định trên khoảng \( (a;b) ​​​) và điểm \( x_0 \in (a ; b )\)

• Hàm số \( f(x) \) đạt cực đại tại \( x_0 \), nếu tồn tại một số\( h>0 \) sao cho \( f( x) ) < f(x_0) \) cho tất cả \( x \in (x_0-h;x_0+h) \) và \(x \neq x_0\)
• Nếu tồn tại một số\( h>0 \) sao cho \( f(x) >; f(x_0) \) với mọi \( x \in (x_0-h;x_0 +h ) \) và \(x \neq x_0\)

Lý thuyết:

Hàm số \( y=f(x) \) liên tục, xác định và có đạo hàm cấp hai trên khoảng \( (a;b) ​​​). sau đó

• Nếu \(\left\{\begin{matrix} f'(x_0)=0\\ f”(x_0)>0 \end{matrix}\ \rightarrow\) \( x_0 \) là điểm cực tiểu của hàm số \( f \)
• If \(\left\{\begin{matrix} f'(x_0)=0\\ f”(x_0)<0 \end{matrix}\right. rightarrow\) \( x_0 \) là điểm cực đại của hàm số\( f \)

Chi tiết>> Giá trị cực trị của hàm số là bao nhiêu?

Cực trị của hàm số bậc hai?

Định nghĩa cực trị của hàm số bậc hai

Đối với hàm bậc hai: \( y=f(x) = ax^4+bx^3+cx^2+dx+e \) và \(a \neq 0\)

Đạo hàm \( y’ = 4ax^3+3bx^2+2cx+d \)

Hàm \( y=f(x) \) có thể có một hoặc ba cực trị.

Điểm cực trị là điểm tại đó đạo hàm \( y’ \) đổi dấu

Các giá trị cực trị của hàm bậc hai

Xét đạo hàm \( y’ = 4ax^3+3bx^2+3cx+d \)

• Nếu \( y’=0 \) có đúng 1 nghiệm thì hàm số \( y=f(x) \) có đúng 1 điểm cực trị (có thể là giá trị lớn nhất hoặc nhỏ nhất). ) .
• Nếu \( y’=0 \) có 2 nghiệm (gồm 1 nghiệm đơn và 1 nghiệm kép) thì hàm số \( y=f(x) \) có đúng 1 giá trị cực (có thể .là giá trị lớn nhất hoặc nhỏ nhất).
• Nếu \( y’=0 \) có 3 nghiệm khác nhau thì hàm số \( y=f(x) \) có 3 giá trị cực trị (kể cả cực đại và cực tiểu).

Ví dụ:

Chứng minh rằng hàm \( f(x) = x^4+mx^3+mx^2+mx+1 \) không thể dùng cho mọi \( m \in \mathbb{r }\)

Xem Thêm : File INDD là gì?

Giải pháp:

Để chứng minh một hàm số đã cho không có cả giá trị lớn nhất và giá trị nhỏ nhất, ta chứng minh rằng hàm số đối với mỗi \(m \in \mathbb{r}\ )

Xét đạo hàm \( f'(x)=4x^3+m(3x^2+2x+1) \)

Xét phương trình \(f'(x)= 0 \leftrightarrow 4x^3+m(3x^2+2x+1)=0\)

\(\leftrightarrow \frac{4x^3}{3x^2+2x+1}+m=0\)

Xét hàm \( g(x) =\frac{4x^3}{3x^2+2x+1}+m\)

Ta có:

\(g'(x) =\frac{12x^2(3x^2+2x+1)-4x^3(6x+2)}{(3x^2+2x+1)^ 2}\)

\(=\frac{4x^2(3x^2+4x+3)}{(3x^2+2x+1)^2} \geq 0 \;\;\; \; \forall x \in \mathbb{r}\)

\(\rightarrow\) hàm \( g(x) \) hiệp biến

Phương trình \(\rightarrow\) \( g(x) =0 \) có đúng 1 nghiệm duy nhất

Vậy phương trình \(f'(x)= 0 \) có đúng 1 nghiệm duy nhất

\(\rightarrow\) hàm \( f(x) \) chỉ có một điểm cực trị

Cực trị của hàm bậc hai

Định nghĩa hàm số bậc hai là gì?

Hàm bậc hai là hàm bậc hai có dạng:

\( y=f(x) = ax^4+bx^2+c \)

Vì vậy, chúng ta có thể coi nó như một hàm bậc hai với \( x^2 \) ẩn \( x^2 \)

Cực trị của hàm bậc hai



Ví dụ:

Đối với hàm \( f(x) = 3mx^4+ (m-2)x^2 +m-1 \) . tìm \( m \) sao cho hàm số đã cho có ba điểm cực trị

Xem Thêm : File INDD là gì?

Giải pháp:

Để hàm số \( f(x) \) có 3 điểm cực trị thì

\(3m(m-2)<0\)

\(\leftrightarrow m \in (0;2)\)

Công thức giá trị cực trị của hàm bậc hai

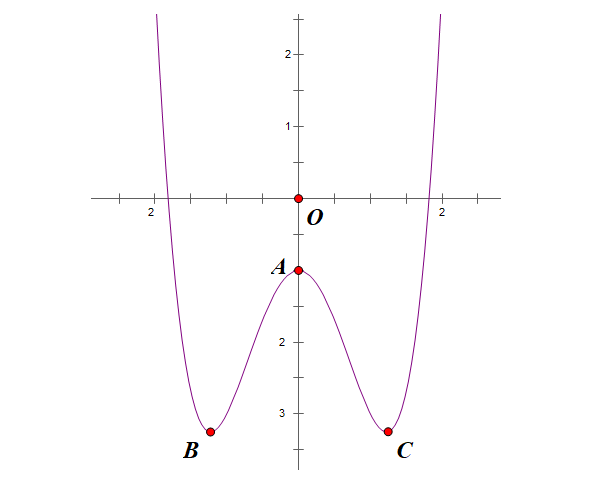
Xét hàm bình phương \( f(x)=ax^4+bx^2+c \) ba điểm cực trị tạo thành một tam giác cân \( abc \) đỉnh \( a \)



Tọa độ đỉnh:

• \(a(0;c)\)
• \(b(-\sqrt{\frac{-b}{2a}};-\frac{\delta}{4a})\)
• \(c(\sqrt{\frac{-b}{2a}};-x\frac{\delta}{4a})\)

Để giải nhanh bài toán hàm số bậc hai trong câu hỏi trắc nghiệm, ta có công thức sau

\(\cos \widehat{bac}=\frac{b^3+8a}{b^3-8a}\)

Diện tích \(\delta abc =\frac{b^2}{4|a|}.\sqrt{-\frac{b}{2a}}\)





Ví dụ:

Đối với hàm \( f(x) = x^4-2mx^2 +3 \) . Tìm \( m \) để đồ thị của hàm số \( f(x) \) có 3 điểm cực trị tạo thành một tam giác cân có độ dài cạnh bên bằng 2 lần độ dài cạnh đáy

Xem Thêm : File INDD là gì?

Giải pháp:

Đối với hàm số có 3 điểm cực trị, \( -2m 0 \)

Theo định luật cosin ta có:

\(bc^2=ab^2+ac^2-2ab.ac.\cos \widehat{bac}\)

\(\leftrightarrow \cos \widehat{bac}=\frac{ab^2+ac^2-bc^2}{2ab.ac}\)

Bởi vì \( \delta abc \) nằm ở \(a\rightarrow ab=ac\)

Theo đề ta có \( ab=2bc \)

Chúng ta có thể thay thế nó

\(\cos \widehat{bac}=\frac{7}{8}\)

Áp dụng công thức \(\cos \widehat{bac}\) ta có:

\(\frac{7}{8}=\cos \widehat{bac}=\frac{b^3+8a}{b^3+8a}=\frac{-8m ^3+8}{-8m^3-8}\)

\(\leftrightarrow m^3=15\leftrightarrow m =\sqrt[3]{15}\) (hài lòng)

Vậy \(m =\sqrt[3]{15}\)

Bài tập về cực trị của hàm bậc hai

Bài 1:

Tìm \( m \) để đồ thị của hàm số\( f(x) = 2x^4-m^2x^2+m^2-1 \) có 3 điểm cực trị\ ( a,b,c \) có 4 điểm\( o,a,b,c \) là 4 đỉnh của hình thoi

A. \( m=\pm \sqrt{2} \)

\( m=\pm \sqrt{3} \)

\( m=\pm 2 \)

Xem Thêm : Điều khác biệt của chương trình đào tạo quốc tế cấp trung học sở 

\( m=\pm 3 \)

\(\mũi tên bên phải a\)

Bài 2:

Tìm \( m \) để đồ thị của hàm số\( f(x) = x^4-2m^2x^2+m^4+1 \) có 3 điểm cực trị\ ( a,b,c \) làm cho bốn điểm\( o,a,b,c \) nằm trên cùng một đường tròn

A. \(m=\pm 1\)

\(m=\pm 2\)

\(m= 1 \)

\(m= -1\)

\(\mũi tên sang phải \)

Bài 3:

Tìm \( m \) để đồ thị hàm số \( f(x)= x^4-2mx^2+m \) có 3 điểm cực trị\( a,b,c ) Lập tam giác có bán kính đường tròn nội tiếp lớn hơn 1

A. \(m \in (2;+\infty)\)

\(m \in (-2;+\infty)\)

\(m \in (-\infty;2)\)

\(m \in (-\infty;-2)\)

\(\mũi tên bên phải a\)

Bài 4:

Tìm \( m \) để đồ thị của hàm số\( f(x)= x^4-2x^2+m+2 \) có 3 điểm cực trị\( a,b , c \) tạo thành một tam giác có tâm là \( o \)

A. \(m=-\frac{2}{3}\)

\(m=-\frac{4}{3}\)

\(m=\frac{2}{3}\)

\(m=\frac{4}{3}\)

\(\mũi tên phải b\)

Bài 5:

Tìm \( m \) để đồ thị hàm số \( f(x)= x^4-2(1-m^2)x^2+m+1 \) có 3 các giá trị cực trị ( a,b,c \) tạo thành tam giác có diện tích lớn nhất

A. \(m=-1\)

\(m=1\)

\(m=0\)

\(m=2\)

\(\mũi tên phải c\)

Bài viết trên của dinhnghia.vn giúp các bạn tổng hợp lý thuyết và bài tập về chủ đề cực trị của hàm số bậc hai có lời giải. Mong rằng những kiến ​​thức trong bài sẽ giúp ích cho các bạn trong quá trình học tập và nghiên cứu về bài toán cực trị của hàm số bậc hai, chúc các bạn học tập vui vẻ!

Xem thêm>>> Bài toán giới hạn của hàm số bậc ba

Xem thêm>>> Tìm m để hàm số có 3 cực trị