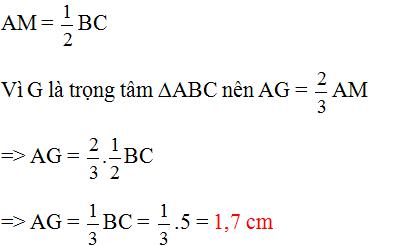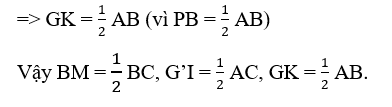Cùng xem Giải toán lớp 7 SGK tập 2 trang 65, 66, 67 chính xác nhất – Tailieu.com trên youtube.

SGK trang 65, 66, 67, Hướng dẫn giải bài tập Toán 4: Tính chất ba đường trung tuyến của một tam giác được giới thiệu chi tiết dưới đây rất dễ hiểu, giúp các bạn tham khảo và sử dụng giải pháp hiệu quả nhất cho cùng một vấn đề toán học.

Đáp án bài toán trang 65 tập 7 bài 2 trang 4

Vẽ một tam giác và tất cả các đường trung tuyến của nó.

Giải pháp

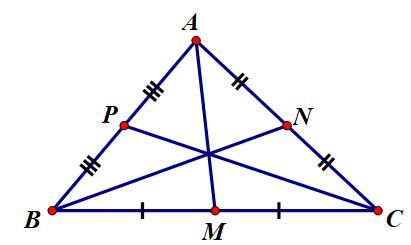
Ta vẽ đồ thị abc và 3 trung tuyến am, bn, cp

Trong đó: m, n, p lần lượt là trung điểm của bc, ac, ab

Trả lời câu hỏi Toán 7 sgk Tập 2 Bài 4 Trang 65

Hãy nhìn vào hình tam giác đã cắt (trên đó vẽ ba đường trung tuyến). Cho biết: Ba đường trung tuyến của tam giác này có cùng đi qua một điểm không?

Giải pháp

Ba đường trung tuyến của tam giác này có chung một điểm

Đáp án Toán lớp 7 Tập 2 Bài 4 Trang 66

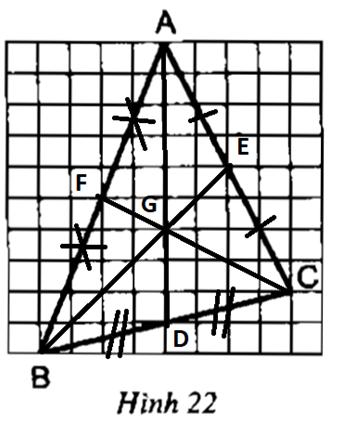
Dựa vào hình 22, hãy cho biết:

• ad có phải là trung tuyến của tam giác abc không?

• Điểm

Bao nhiêu?

Giải pháp

• ad là đường trung tuyến của tam giác abc

Vì trong Hình 22 ta thấy d là trung điểm của bc

(bd = cd = 4 đơn vị độ dài)

• Dựa trên những hình ảnh mà chúng ta đã thấy:

Trả lời câu 23 trang 66 tập 2 SGK Toán 7

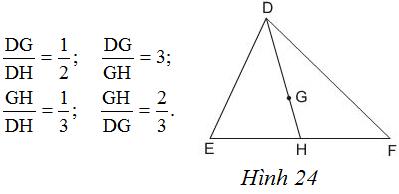
Gọi g là trọng tâm tam giác def có trung tuyến dh.

Phát biểu nào sau đây là đúng?

Xem Thêm : Giải bài 3 vật lí 12: Con lắc đơn – Tech12h

Giải pháp thay thế:

Giải bài 24 trang 66 SGK Toán 7 Tập 2

Đối với Hình 25. Điền số thích hợp vào chỗ trống trong các đẳng thức sau:

a) mg = … mr; gr = … mr; gr = … mg

b) ns = … ng; ns = … gs; ng = … gs

Vượt 25

Xem Thêm : Giải bài 3 vật lí 12: Con lắc đơn – Tech12h

Giải pháp thay thế:

Từ hình vẽ ta thấy: s, r là trung điểm của hai đoạn thẳng trong tam giác nên ns, mr là hai trung tuyến.

g là giao điểm của hai trung tuyến nên g là trọng tâm của Δmns nên ta nhập:

Giải toán 7 tập 2 bài 25 trang 67 SGK

Biết: Trong tam giác vuông. Đường trung trực của cạnh huyền bằng một nửa cạnh huyền. Vui lòng giải quyết các vấn đề sau:

Xem Thêm : Chợ đêm Bavet Mộc Bài – Địa điểm du lịch lý tưởng cho bạn

Cho tam giác vuông abc có hai góc vuông ab=3cm, ac=4cm. Tính khoảng cách từ đỉnh a đến trọng tâm g của tam giác abc.

Xem Thêm : Giải bài 3 vật lí 12: Con lắc đơn – Tech12h

Giải pháp thay thế:

Áp dụng định lý Pitago cho bình phương abc tại a:

bc2 = ab2 + ac2 = 32 + 42 = 25

=>bc = 5cm

Gọi m là trung điểm của bc và g là trọng tâm của Δabc.

Bằng thư:

ma​toán 7 tập 2 bài 26 trang 67 sgk

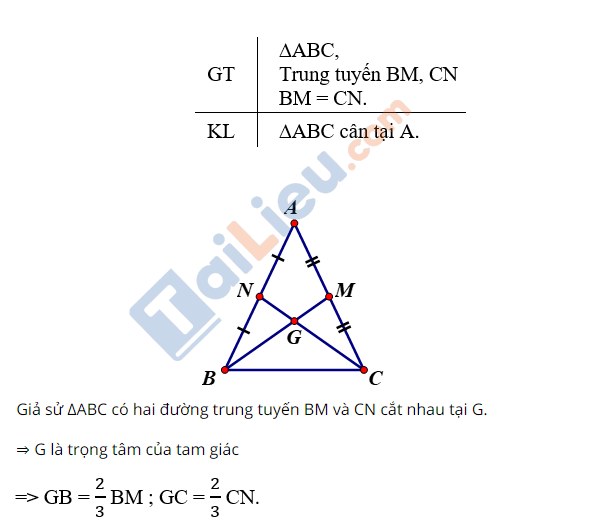
Chứng minh định lý: Trong một tam giác cân, hai đường trung trực tương ứng với hai cạnh bằng nhau.

Xem Thêm : Giải bài 3 vật lí 12: Con lắc đơn – Tech12h

Giải pháp thay thế:

Δabc cân => ab = ac

Gọi m, n lần lượt là trung điểm của các cạnh ab, ac, suy ra:

an = bn = am = cm (= ab/2 = ac/2)

Cách 1: Xét bam, bạn có thể có:

– góc nam a

-ab = ac

-i = a

=> Δbam = Δcan (c.g.c) => bm = cn (dpcm)

Cách 2: Xét bcm và cbn:

– cạnh bc công cộng

– góc bcm = góc cbn (có trọng số abc)

– cm = bn

=> Δbcm = Δcbn (c.g.c) => bm = cn (dpcm)

(Còn nhiều cách chứng minh khác nhưng do kiến ​​thức lớp 7 có hạn nên mình sẽ không giới thiệu lần lượt).

SGK Toán 7 tập 2 trang 67 câu 27

Chứng minh điều ngược lại của định lý trên: Một tam giác cân nếu hai đường trung tuyến của nó bằng nhau.

Xem Thêm : Giải bài 3 vật lí 12: Con lắc đơn – Tech12h

Giải pháp thay thế:

SGK Toán 7 tập 2 trang 67 câu 28

Cho tam giác cân có đường trung bình di tại d.

a) Chứng minh rằng dei = dfi.

b) Góc die và dif là gì?

c) Cho de = df = 13cm, ef = 10cm, tính độ dài trung tuyến di.

Xem Thêm : Giải bài 3 vật lí 12: Con lắc đơn – Tech12h

Giải pháp thay thế:

a) Xem xét dei và dfi với:

– de = df (Δdef cân bằng)

– di là cạnh chung.

– ie = if (di là trung tuyến)

=> Δdei = Δdfi (c.c.c)

(Hoặc: nếu thay điều kiện di là cạnh chung bằng góc dei = góc dfi thì ta có cách chứng minh theo c.g.c)

b) Từ câu a) ta có dei = dfi

c) i là trung điểm của ef nên ie = if = 5cm

Δdie vuông tại i => di2 = de2 – ei2 (Định lý Pitago)

=>di2 = 13² – 5² = 144

=>di = 12

SGK Toán 7 tập 2 trang 67 câu 29

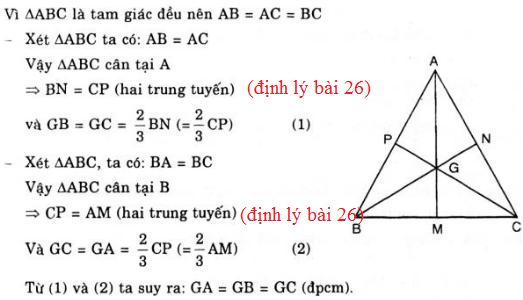
Gọi g là trọng tâm tam giác đều abc. Bằng chứng:

ga = gb = gc

Hướng dẫn: Áp dụng định lý bài tập 26.

Xem Thêm : Giải bài 3 vật lí 12: Con lắc đơn – Tech12h

Giải pháp thay thế:

Gọi m, n, p lần lượt là trung điểm của các cạnh bc, ac, ab.

(Lưu ý: Bài này cần áp dụng định lý ở bài tập 26 nên một số sách hay trang web giải toán sử dụng “Vì Δabc chính quy nên ba đường trung tuyến tương ứng với ba cạnh bc,ca,ab bằng nhau” Câu này không áp dụng cho bài tập này, xin lưu ý.)

Giải bài 30 Trang 67 SGK Toán 7

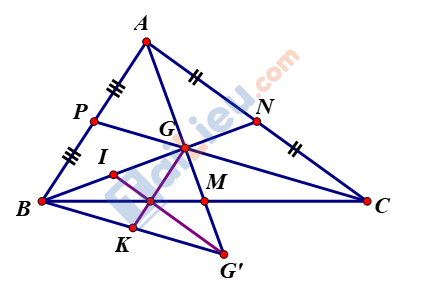
Gọi g là trọng tâm của tam giác abc. Lấy điểm g’ trên tia ag sao cho g là trung điểm của ag’.

a) So sánh các cạnh của tam giác bgg’ với đường trung bình của tam giác abc.

b) So sánh đường trung bình của tam giác bgg’ với các cạnh của tam giác abc.

Xem Thêm : Giải bài 3 vật lí 12: Con lắc đơn – Tech12h

Giải pháp thay thế:

Vậy mỗi cạnh của Δbgg’ bằng 2/3 giá trị trung vị của Δabc.

b) Gọi i, k là trung điểm của bg và bg’.

Vì vậy, mỗi trung tuyến của Δbgg’ bằng một nửa cạnh Δabc tương ứng của nó.

Nhấn nút Tải xuống bên dưới ngay bây giờ để tải gaiir toán lớp 7 trang 65, 66, 67 file word, pdf hoàn toàn miễn phí

Nguồn: https://dongnaiart.edu.vn
Danh mục: Tin tức

Lời kết: Trên đây là bài viết Giải toán lớp 7 SGK tập 2 trang 65, 66, 67 chính xác nhất – Tailieu.com. Hy vọng với bài viết này bạn có thể giúp ích cho bạn trong cuộc sống, hãy cùng đọc và theo dõi những bài viết hay của chúng tôi hàng ngày trên website: Dongnaiart.edu.vn