Bạn đang xem: Bất phương trình bậc nhất hai ẩn – Lý thuyết và bài tập ứng dụng Tại DongnaiArt

Bất phương trình bậc nhất hai ẩn là một phần vô cùng quan trọng trong chương trình toán học. và sẽ được sử dụng trong suốt toán học. Bạn có thể đọc các bài viết dưới đây của chúng tôi để hoàn thành xuất sắc khóa học này.

1. Hai bất phương trình bậc nhất một ẩn

1.1 – Khái niệm

Hai bất phương trình bậc nhất chưa biết sẽ có dạng tổng quát như sau: ax + by ≤ c

Ở đâu:

• a,b,c là các số đã cho.
• x, y là các ẩn số cần tìm.

Tiền đề là a và b không thể bằng 0.

Cặp số (x0;y0) là cặp nghiệm của bất phương trình bậc nhất 2 ẩn ax+by≤c thỏa mãn điều kiện ax0+by0≤c.

1.2 – Miền giải pháp

• Định nghĩa

Tập hợp tất cả các điểm trên mặt phẳng tọa độ Oxy sẽ có một xạ là nghiệm của bất phương trình ẩn kép hay còn gọi là miền nghiệm của bất phương trình.

• Lý thuyết
• Phương pháp giải bất phương trình bậc nhất hai ẩn là:

Để đại diện cho một miền giải pháp, bạn phải có thể làm theo các bước sau:



1.3. Hệ bất phương trình bậc nhất hai ẩn là gì?



Điểm 8+ cho kiến ​​thức của bạn về bất phương trình bậc hai hai ẩn và cách áp dụng chúng vào toán học một cách dễ dàng. Nhấp vào đây để tìm hiểu thêm về khóa học này: Đột phá môn Toán lớp 10 8+. Đồng hành cùng bạn là một giáo viên vững vàng với hơn 6 năm kinh nghiệm giảng dạy và luyện thi. Đặc biệt, đăng ký Ant House ngay hôm nay bạn sẽ được giảm 73% học phí!

2. Hướng dẫn giải bài 4 Bất phương trình bậc nhất hai ẩn sgk

2.1 – Trang 96 Câu 1

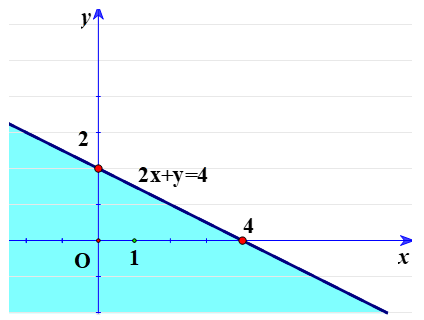
Hãy biểu diễn dạng hình học đã học cho hai bất phương trình bậc nhất chưa biết sau: -3x + 2y > 0

Hướng dẫn giải pháp:

Ta sẽ vẽ đường thẳng (d): -3x + 2y = 0



Tiếp theo ta lấy điểm a(1; 1), thấy a ∉(d) và có: -3.1 + 2.1 <;0 Suy ra nửa mặt phẳng bờ (d) không chứa a là nghiệm miền bất phương trình. Hoặc một khu vực của hình ảnh không được tô sáng trong hình trên.

2.2 – Trang 97 Câu 2

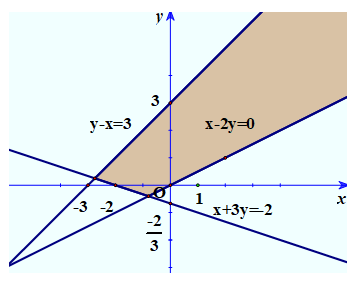
Kí hiệu biểu thức hình học của hệ bất phương trình bậc nhất sau:



Hướng dẫn giải pháp:





Ta lấy điểm o(0,0), thấy o không thuộc 2 đường thẳng trên, có 2.0-0 3 và -2.0 + 0 8/5 nên suy ra phần hữu hạn. bằng hai đường chứa điểm o Phần trên là phần không có bóng.

Đây là nghiệm của bất phương trình.

2.3 – Bài 1 trang 99

Kí hiệu tập nghiệm của bất phương trình bậc hai sau:



Hướng dẫn giải pháp:

a) Ta có:



Tương đương với -x + 2y – 4 < 2 – 2x

Đổi vế ta được bất phương trình sau: x + 2y <; 4

Tập nghiệm của phương trình đã cho là nửa mặt phẳng được tô màu trong hệ tọa độ Oxy.

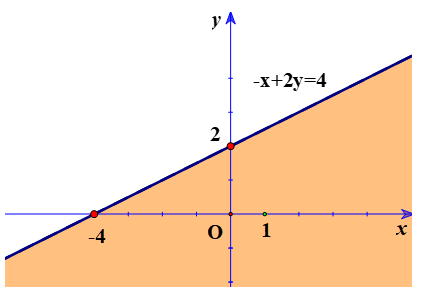
b) Ta có:

3(x-1) + 4(y-2)

5x – 3

Tương đương với 3x – 3 + 4y -2 < 5x – 3

Sau khi đổi vế ta được bất phương trình sau: -x + 2y <; 4

Tập nghiệm của bất phương trình được biểu diễn trên các trục tọa độ như sau:

2.4 – Bài 2 trang 99

Xem Thêm : giới thiệu truyện conan bằng tiếng anh



Hướng dẫn giải pháp:

a) Miền nghiệm của hệ bất phương trình trên sẽ được biểu diễn bởi hệ tọa độ sau:



b) Giải các bất phương trình sau

Đó là mặt phẳng được biểu diễn bởi giản đồ Oxy bên dưới.

Chúng tôi sẽ xóa 1 ngân hàng, tức là x/3 + y/2 = 1 hàng

2.5 – Bài 3 trang 99

Hướng dẫn giải pháp:

Hãy gọi các nhà máy sản xuất x và y lần lượt là sản phẩm i và sản phẩm ii. Thỏa mãn điều kiện x,y >= 0.

Ta có, tổng lợi nhuận là l = 3x + 5y (nghìn đồng).

Theo đề bài ta có:

Nhóm a cần máy 2x + 2y

Nhóm b yêu cầu máy 2y và máy 2x + 4y.

=>Ta có bất đẳng thức sau:



Miền nghiệm của hệ bất phương trình trên là miền đa giác abcod, có tọa độ lần lượt là a(4;1), b(2;2), c(0,2); o(0,0); d (5,0 ). l sẽ đạt giá trị lớn nhất tại một trong các đỉnh sau:

Chúng tôi có một bảng:

Theo bảng trên, khi x=4 và y=1 thì lmax = 17

=>Để có thể sản xuất 2 sản phẩm trên với lợi nhuận cao nhất, hãng sẽ cần 4 sản phẩm i và 1 sản phẩm ii.

Chúng ta có một hệ tọa độ:



3. Gợi ý giải một số bài tập sbt

3.1 – Bài 4.46 sbt trang 116 Toán 10

Hãy biểu diễn hình học nghiệm của bất phương trình sau:

a) 3 + 2y > 0;

b) 2x – 1 <;0;

c) x – 5y < 2;

d) 2x + y > 1;

e) -3x + y + 2 0;

e) 2x – 3y + 5 0.

Hướng dẫn giải pháp:

a) Điểm o(0,0) có tọa độ thỏa mãn bất phương trình nên miền nghiệm là nửa mặt phẳng bờ 3 + 2y = 0 chứa o.

b) Miền nghiệm là nửa mặt phẳng cạnh 2x – 1 = 0 chứa o.

c) Miền nghiệm là nửa mặt phẳng có cạnh -x + 5y = -2 chứa o.

d) Miền có nghiệm là nửa mặt phẳng cạnh 2x + y = 1 không chứa o.

e) Miền nghiệm của nửa mặt phẳng có cạnh -3x + y = -2 không chứa o.

f) Miền nghiệm chính là nửa mặt phẳng bờ 2x – 3y = -5 chứa điểm o.

3.2 – Bài 4.47 trang 116 SGK Toán 10

Một nông dân trồng đậu và cà tím trên mảnh đất 8a. Nếu trồng đậu cần 20 lao động, thu nhập 3 triệu đồng/năm, trồng cà tím cần 30 lao động, thu nhập 40 triệu đồng/năm. Câu hỏi đặt ra là nếu tổng số công nhân không quá 180 người thì diện tích trồng mỗi loại cây là bao nhiêu để thu được nhiều lợi nhất?

Hướng dẫn giải pháp:

Xem Thêm : Tính chất hoá học của Oxit, Axit, Bazo và Muối – Hoá lớp 9

Gọi x là diện tích của chiếc đậu và y là diện tích của quả cà tím, (đơn vị a = 100 m2).

Điều kiện là x 0, y 0, ta có x + y ≤ 0

Nỗ lực cần thiết là 20x + 30y ≤ 180 hoặc 20 + 3y ≤ 18

Suy ra số tiền sẽ bị tính phí

f = 3000000x + 4000000y (Đồng Việt Nam)

hoặc f = 3x + 4y (phía đông)

Ta cần tìm x,y thỏa mãn hệ bất phương trình



f = 3x + 4y cần đạt giá trị lớn nhất.

Ta kí hiệu tập nghiệm của (h) sẽ là tứ giác oabc với a(0;6), b(6;2), c(8,0) và o(0,0).



Khi so sánh giá trị của f tại các đỉnh o, a, b, c ta sẽ suy ra x=6, y=2 (tọa độ điểm b) là diện tích có thể trồng được từng loại .Số tiền thu được nhiều nhất là f = 26 (Triệu đồng).

Như vậy ta sẽ trồng được 6a đậu, 2a cà chua, thu được 26 000 000 đồng.

<3



A. x+2y＞3

2x + y 3

2x + y < 3

x + y – 3 0

Hướng dẫn giải pháp:

Chọn b

<3



Hướng dẫn giải pháp:

Đáp án: c

5 – Bài 4.50: Trong các câu sau, câu nào đúng?



A. Miền không giao nhau của Hình 45, bao gồm cả các biên, sẽ biểu diễn miền nghiệm của bất phương trình x + y ≤ 2.

Hình 45 Miền không giao nhau, kể cả biên, sẽ biểu thị miền nghiệm của bất phương trình

và (x; y) = (-1; 1) là nghiệm của hệ.

Vùng không giao nhau trong Hình 45, bao gồm cả các biên, sẽ biểu thị miền nghiệm của bất phương trình, (x;y) = (-2;1) là một nghiệm của hệ.

D. Hình 45 với miền không bị gạch, kể cả biên sẽ biểu diễn được miền nghiệm của bất phương trình 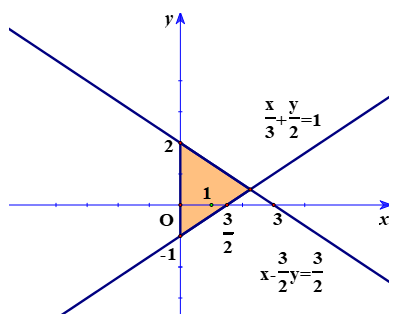và (x; y) = (1; 0) là một nghiệm của hệ.

Hướng dẫn giải pháp: f

Đáp án: đ

=>>Xem thêm nội dung liên quan: phương trình bậc hai và cách giải

Trên đây là toàn bộ nội dung mà chúng tôi muốn gửi đến bạn. Vui lòng tham khảo bất đẳng thức bậc nhất này cho hai ẩn số này có thể được thực hiện độc đáo. Hi vọng bài viết trên sẽ giúp ích cho các bạn trong quá trình học toán.

Đăng ký tại đây=>>> guru<<=Nhận các khóa học chất lượng cao giúp trẻ phát triển học tập tốt hơn