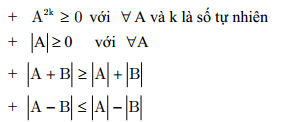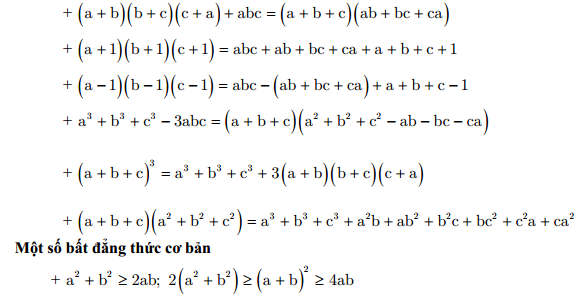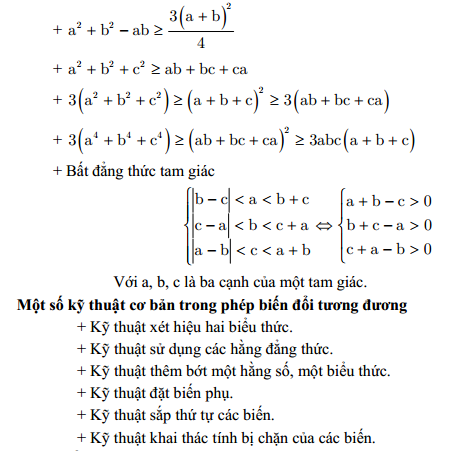Bạn đang xem: Các phương pháp chứng minh bất đẳng thức (có lời giải chi tiết) Tại DongnaiArt

Tài liệu bao gồm các phương pháp chứng minh bất đẳng thức từ cơ bản nhất đến nâng cao. Mỗi bài đều có phân tích và đáp án chi tiết, rất hữu ích cho các bạn.

Chương Một. Một số giải pháp

chủ đề 1 Kĩ thuật biến đổi đẳng thức chủ đề 3 chủ đề 2 Sử dụng tính chất của tỉ số, giá trị tuyệt đối và tam thức bậc hai để chứng minh bất đẳng thức 44 1. Sử dụng tính chất của tỉ số 45 2. Sử dụng tính chất của giá trị tuyệt đối 54 3. Sử dụng tam thức bậc hai Tính chất của hàm số. 59 Chủ đề 3 Chứng minh bất đẳng thức bằng cách bác bỏ 68 Chủ đề 4 Chứng minh bất đẳng thức liên quan đến tổng và tích của chuỗi – Quy nạp 86 Chủ đề 5 Kỹ thuật sử dụng bất đẳng thức Cauchy 117 1. Kỹ thuật chọn điểm rơi trong đánh giá trung bình-trung bình 118 2. Kỹ thuật chọn điểm rơi là trung bình đến trung bình trong đánh giá. 141 3. Kỹ thuật chỉnh hợp trong bất đẳng thức Cauchy 161 4. Kỹ thuật cộng trừ 175 5. Kỹ thuật phản Cauchy 191 6. Kỹ thuật biến đổi biến 199 Chủ đề 6 Kỹ thuật sử dụng bất đẳng thức bunhiacopxki 220 1. Kỹ thuật chọn điểm thả 221 2. Sử dụng các dạng cơ bản Kỹ thuật của bất đẳng thức bunhiacopxki 236 3. Kỹ thuật sử dụng bất đẳng thức bunhiacopxki ở dạng phân số 252 4. Kỹ thuật cộng trừ 275 5. Kỹ thuật đổi biến trong bất đẳng thức bunhiacopxki 289

Chương Hai. Một số kỹ năng giải toán hayChủ đề 7 Áp dụng nguyên lý Dirichlet để chứng minh bất đẳng thức 307 Chủ đề 8 Hệ số bất định để chứng minh bất đẳng thức 319 Chủ đề 9 Ứng dụng có hệ thống các kết quả bất đẳng thức Schur 333 Chủ đề 10 Ứng dụng và các bài toán về đạo hàm trong chứng minh bất đẳng thức 344

Hãy tìm các điểm cực trị. 1. Bố cục bằng kỹ thuật sử dụng bất đẳng thức cổ điển 344 2. Bố cục bằng kỹ thuật biến đổi tổ hợp. 405

Chương ba. Chọn một số bài toán bất đẳng thức. Chap 649

MỘT SỐ KIẾN THỨC CƠ BẢN VỀ BẤT ĐẲNG THỨC I. Định nghĩaGiả sử A và B là hai biểu thức bằng số hoặc bằng chữ. Khi đó +) \(A > B;A < B;A \ge B;A \le B\) được gọi là các bất đẳng thức. + \(A – B > 0;A – B < 0;A – B \ge 0;A – B \le 0\) Các bất đẳng thức trên được viết lại như sau + Một bất đẳng thức bất kì có thể đúng, cũng có thể sai. Quy ước: Khi nói về một bất đẳng thức mà không nói gì thêm thì ta hiểu đó là một bất đẳng thức đúng.

Xem Thêm : Sơn Tĩnh Điện Xe Máy Tại Tp. Hồ Chí Minh

Một số phương pháp chứng minh bất phương trình chương 1Nội dung cơ bản của chương 1 gồm: ·Giới thiệu các phương pháp chứng minh bất phương trình. · Nêu một số tính chất liên quan và chứng minh một số nhận xét của các bất đẳng thức trên. · Giới thiệu quy trình giải bài tập mẫu và suy luận phân tích, hướng dẫn giải chi tiết. · Giới thiệu một số bài tập tự luyện.

Xem Thêm : những hình ảnh về người mẹ

Tất cả nội dung bài viết. Vui lòng xem thêm và tải về các tài liệu chi tiết sau:

Tải xuống

Bài tập trắc nghiệm môn Toán lớp 10 – Xem ngay