Cùng xem Công thức tính đường cao trong tam giác – Thủ Thuật Phần Mềm trên youtube.
Bạn cần tính chiều cao của tam giác nhưng lại không nhớ công thức tính chiều cao của tam giác. Vậy hãy tham khảo bài viết sau để biết công thức và cách tính chiều cao của hình tam giác nhé.
Sau đây là công thức tính chiều cao của tam giác, mời các bạn theo dõi.
Chiều cao của hình tam giác?
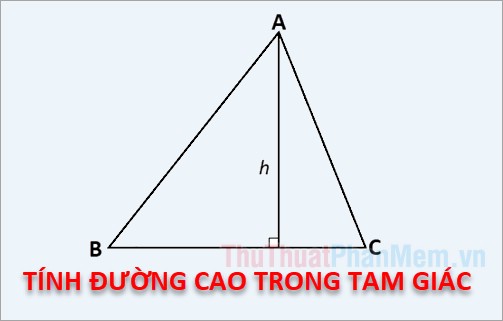
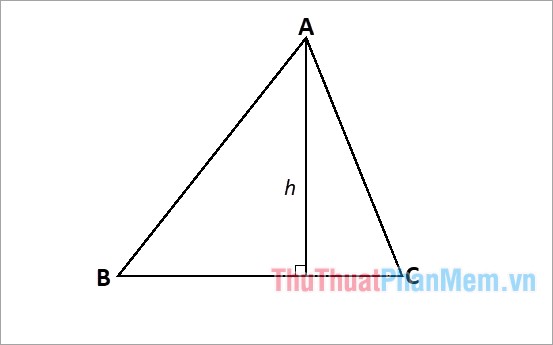
Chiều cao của một tam giác là đoạn thẳng kẻ từ đỉnh này đến cạnh đối diện. Cạnh đối diện này được gọi là đường đáy tương ứng với đường cao. Độ dài đường cao chính là khoảng cách giữa đỉnh và đáy.
Công thức tính chiều cao của hình tam giác
Có nhiều cách giúp bạn tính chiều cao, một cách dễ dàng để tính chiều cao của hình tam giác là sử dụng công thức heron:
\[{h_a} = 2\frac{{\sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left ( {p – c} \right)} }}{a}\]
trong đó a, b, c là độ dài các cạnh; ha là độ dài từ đỉnh a đến cạnh bc đường cao được vẽ; p là nửa chu vi:
\[p = \frac{{\left({a + b + c} \right)}}{2}\]
Công thức tính chiều cao của tam giác đều
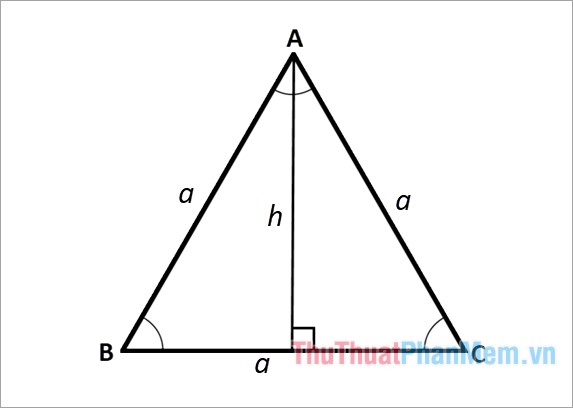
Giả sử một tam giác đều abc có các cạnh bằng a như sau:
Xem Thêm : Thơ tán gái hay nhất mọi thời đại khiến nàng đổ trong giây lát
Công thức chiều cao: \(h = a\frac{{\sqrt 3 }}{2}\)
Trong đó: h là chiều cao của tam giác đều; a là độ dài cạnh của tam giác đều.
Công thức tính chiều cao của tam giác vuông
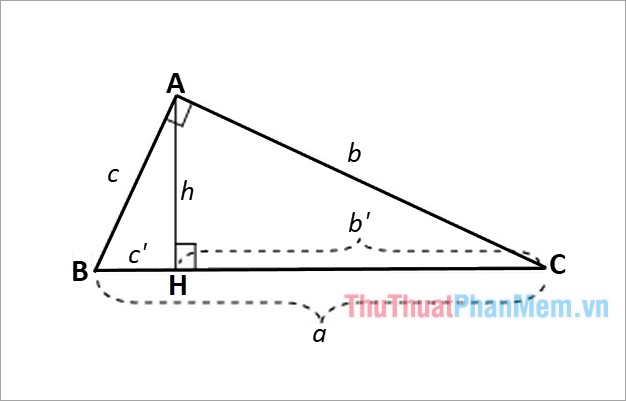
Giả sử có tam giác vuông abc tại a như hình bên:
Công thức tính cạnh và chiều cao của tam giác vuông:
1. \({a^2} = {b^2} + {c^2}\)
2. \({b^2} = a.b’\) và \({c^2} = a.c’\)
3. À = BC
4. \({h^2} = b’.c’\)
5. \(\frac{1}{{{h^2}}} = \frac{1}{{{b^2}}} + \frac{1}{{{c ^2}}} \)
Trong đó: a, b, c là các cạnh của tam giác vuông trong hình trên;
Xem Thêm : Soạn bài Ông lão đánh cá và con cá vàng hay nhất – sách Cánh diều
b’ là hình chiếu của cạnh b trên cạnh huyền; c’ là hình chiếu của cạnh c trên cạnh huyền Hình chiếu trên cạnh;
h là chiều cao của tam giác vuông vẽ từ đỉnh của góc vuông a đến cạnh huyền bc.
Vậy các em có thể dựa vào các công thức tính cạnh và chiều cao trong tam giác vuông trên để giải bài toán.
Công thức tính chiều cao của tam giác cân
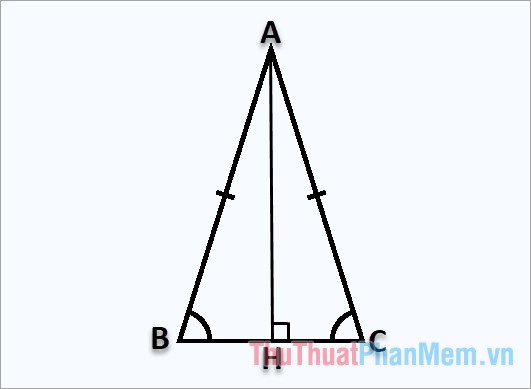
Giả sử bạn có một tam giác cân abc tại a có chiều cao ah vuông góc với h như sau:
Công thức nhiều đường:
Vì tam giác abc là tam giác cân tại a, và đường cao ah cũng là đường trung tuyến nên:
\( \rightarrow hb = hc = \frac{{bc}}{2}\)
Áp dụng định lý Pitago cho tam giác vuông abh tại h, ta có:
\(a{h^2} + b{h^2} = a{b^2}\)
\( \rightarrow a{h^2} = a{b^2} – b{h^2}\)
Trên đây là công thức tính chiều cao của tam giác, các em chỉ cần tính các thành phần chưa biết trong công thức tính chiều cao trong tam giác là có thể tính được chiều cao trong tam giác. chúc may mắn!
Nguồn: https://dongnaiart.edu.vn
Danh mục: Tin tức
Lời kết: Trên đây là bài viết Công thức tính đường cao trong tam giác – Thủ Thuật Phần Mềm. Hy vọng với bài viết này bạn có thể giúp ích cho bạn trong cuộc sống, hãy cùng đọc và theo dõi những bài viết hay của chúng tôi hàng ngày trên website: Dongnaiart.edu.vn
