Bạn đang xem: Công thức toán lớp 5 Tại DongnaiArt

Hệ thống công thức toán lớp 5

DOWNLOAD TÀI LIỆU TỔNG HỢP TOÁN LỚP 5

a. bổ sung

i. công thức chung:

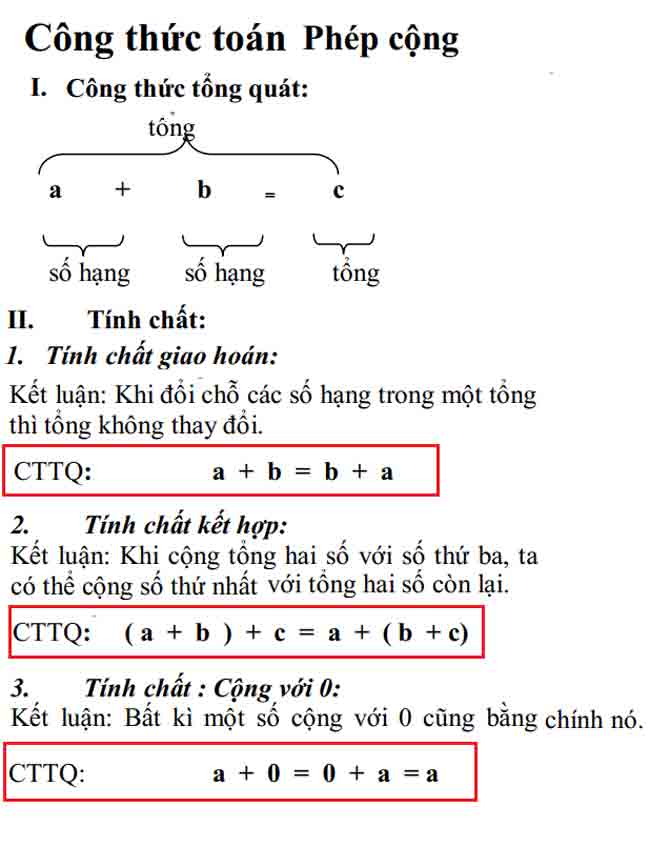
II. Tính chất:

1. thuộc tính giao hoán:

Kết luận: Việc hoán đổi các thuật ngữ trong một tổng không làm thay đổi tổng.

công thức chung: a + b = b + a

2. thuộc tính liên kết:

kết luận: khi chúng ta cộng tổng của hai số với số thứ ba, chúng ta có thể cộng số đầu tiên với tổng của hai số còn lại.

công thức chung: (a + b) + c = a + (b + c)

3. thuộc tính: cộng với 0:

kết luận: bất kỳ số nào cộng với 0 đều bằng chính nó.

cttq: a + 0 = 0 + a = a

B. Phép trừ

i. công thức chung:

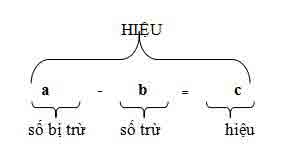
II. Tính chất:

1. trừ 0:

kết luận: bất kỳ số nào nhỏ hơn 0 đều bằng chính nó.

cttq: a – 0 = a

2. trừ chính nó:

kết luận: một số trừ đi chính nó bằng 0.

cttq: a – a = 0

3. trừ một tổng:

Kết luận: Khi trừ một số cho một tổng, chúng ta có thể lấy số đó trừ từng số hạng của tổng đó.

cttq: a – (b + c) = a – b – c = a – c – b

4. trừ một điểm khác biệt:

Kết luận: Khi trừ một số bằng một hiệu, ta có thể lấy số bị trừ cho số bị trừ rồi cộng với số trừ.

cttq: a – (b – c) = a – b + c = a + c – b

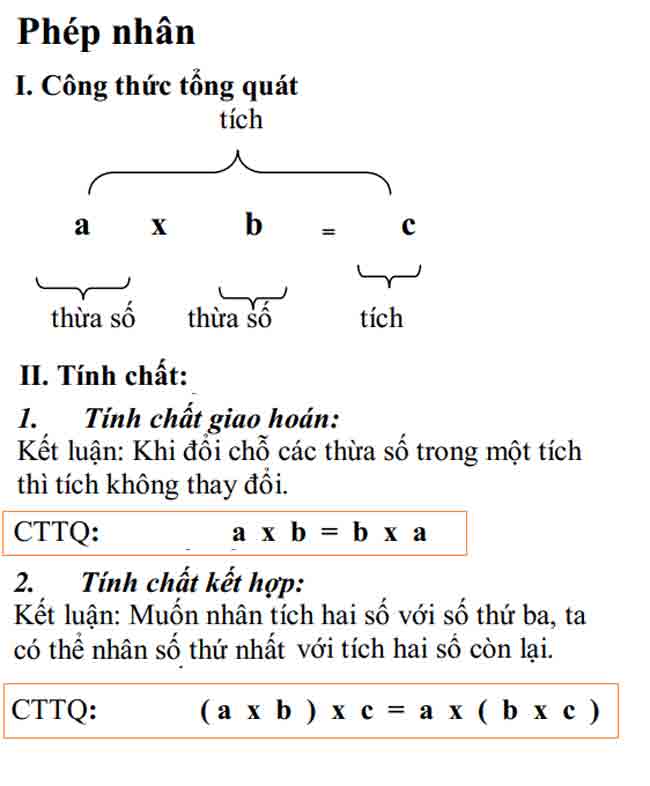
c. phép nhân

i. công thức chung

II. Tính chất:

1. thuộc tính giao hoán:

Kết luận: Việc hoán đổi các yếu tố trong một sản phẩm không làm thay đổi sản phẩm.

cttq: a × b = b × a

2. thuộc tính liên kết:

kết luận: nếu chúng ta muốn nhân hai số với số thứ ba, chúng ta có thể nhân số thứ nhất với tích của hai số kia.

cttq: (a × b) × c = a × (b × c)

3. thuộc tính: nhân với 0:

kết luận: bất kỳ số nào nhân với 0 cũng bằng 0.

cttq: a × 0 = 0 × a = 0

4. nhân với 1:

kết luận: một số nhân với 1 thì bằng chính nó.

cttq: a × 1 = 1 × a = a

5. nhân với một tổng:

Kết luận: Khi nhân một số với một tổng, chúng ta có thể nhân số đó với từng số hạng trong tổng rồi cộng kết quả.

cttq: a × (b + c) = a × b + a × c

6. nhân với một hiệu số:

Kết luận: Khi nhân một số với một hiệu, ta có thể nhân số đó với số bị trừ và số bị trừ rồi trừ hai kết quả.

cttq: a × (b – c) = a × b – a × c

d. sự phân chia

i. công thức chung:

Phép chia còn dư:

a: b = c (phần còn lại r)

thương số phần dư của phép chia

lưu ý: số dư phải nhỏ hơn số chia.

ii. công thức:

1. chia cho 1: bất kỳ số nào chia cho 1 vẫn bằng chính nó.

cttq: a: 1 = a

2. chia cho chính nó: một số chia cho chính nó bằng 1.

cttq: a: a = 1

3. 0 chia cho một số: 0 chia cho bất kỳ số nào khác 0 đều bằng 0

cttq: 0: a = 0

4. một tổng chia cho một số: Khi chia một tổng cho một số, nếu các số hạng của tổng đó chia hết cho số đó thì ta có thể chia từng số hạng cho số bị chia và cộng các kết quả lại với nhau.

cttq: (b + c): a = b: a + c: a

5. hiệu chia cho một số: khi chia hiệu cho một số, nếu số bị trừ và số bị trừ cùng chia hết cho số đó thì ta lấy số bị trừ và số bị trừ chia cho số đó và sau đó trừ hai kết quả cho nhau.

cttq: (b – c): a = b: a – c: a

6. chia một số cho một tích: Khi chia một số cho một tích, chúng ta có thể chia số đó cho một thừa số rồi chia kết quả cho thừa số kia.

cttq: a: (b × c) = a: b: c = a: c: b

7. chia một tích cho một số: Khi chia một tích cho một số, chúng ta có thể chia một thừa số cho số đó (nếu nó là số chia hết) và sau đó nhân kết quả với thừa số kia.

cttq: (a × b): c = a: c × b = b: c × a

p. chia hết

1, chia hết cho 2: Các số kết thúc bằng 0, 2, 4, 6, 8 (số chẵn) chia hết cho 2.

ví dụ: 312; 54768;….

2, chia hết cho 3: số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.

ví dụ: đưa ra số 4572

chúng ta có 4+ 5 + 7+ 2 = 18; 18: 3 = 6 nên 4572: 3 = 1524

3, chia hết cho 4: Các số có hai chữ số cuối cùng chia hết cho 4 thì chia hết cho 4.

ví dụ: cho số: 4572

chúng ta có 72: 4 = 18 nên 4572: 4 = 11 4 3

4, chia hết cho 5: Các số kết thúc bằng 0 hoặc 5 chia hết cho 5.

ví dụ: 5470; 7635

5, chia hết cho 6 (nghĩa là chia hết cho 2 và 3): các số chẵn có tổng chữ số chia hết cho 3 thì chia hết cho 6.

ví dụ: cho số 1356

ta có 1 + 3 + 5 + 6 = 15; 15: 3 = 5 nên 1356: 3 = 452

6, chia hết cho 10 (nghĩa là chia hết cho 2 và 5): Các số tròn (không có đơn vị) chia hết cho 10.

ví dụ: 130; 2790

7, chia hết cho 11: Nếu tổng các chữ số ở hàng chẵn bằng tổng các chữ số ở hàng lẻ thì số đó chia hết cho 11.

ví dụ: cho số 48279

chúng ta có 4 + 2 + 9 = 8 + 7 = 15 nên 48279: 11 = 4389

8, chia hết cho 15 (nghĩa là chia hết cho 3 và 5): Các số có chữ số hàng đơn vị là 0 (hoặc 5) và tổng các chữ số chia hết cho 3 thì chia hết cho 15.

ví dụ: đưa ra số 5820

chúng ta có 5 + 8 + 2 + 0 = 15; 15: 3 = 5 nên 5820: 15 = 388

9, chia hết cho 36 (nghĩa là chia hết cho 4 và 9): hai chữ số cuối cùng chia hết cho 4 và tổng các chữ số chia hết cho 9 chia hết cho 36.

ví dụ: cho số: 45720

chúng ta có 20: 4 = 5 và (4 + 5 + 7 + 2 + 0) = 18

18: 9 = 2 thì 45720: 36 = 1270

f. trung bình cộng

1. nếu chúng ta muốn tìm giá trị trung bình (tbc) của nhiều số, chúng ta tính tổng của các số đó rồi chia tổng đó cho số số hạng.

cttq: tbc = tổng các số: số lượng các điều khoản

2. tìm tổng các số: chúng tôi nhân số hạng với tbc

cttq: tổng các số = tbc × số điều khoản

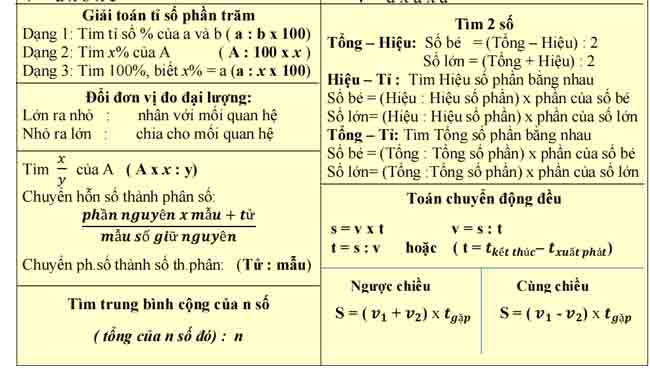
tìm hai số khi bạn biết tổng và hiệu của hai số đó

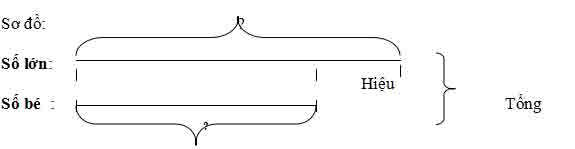
Cách 1:

tìm một số lớn = (tổng + hiệu): 2

tìm số nhỏ = số lớn – chênh lệch

hoặc số nhỏ = tổng – số lớn

dạng 2:

tìm số nhỏ = (tổng – hiệu): 2

tìm số lớn = số nhỏ + hiệu số

hoặc số lớn = tổng – số nhỏ

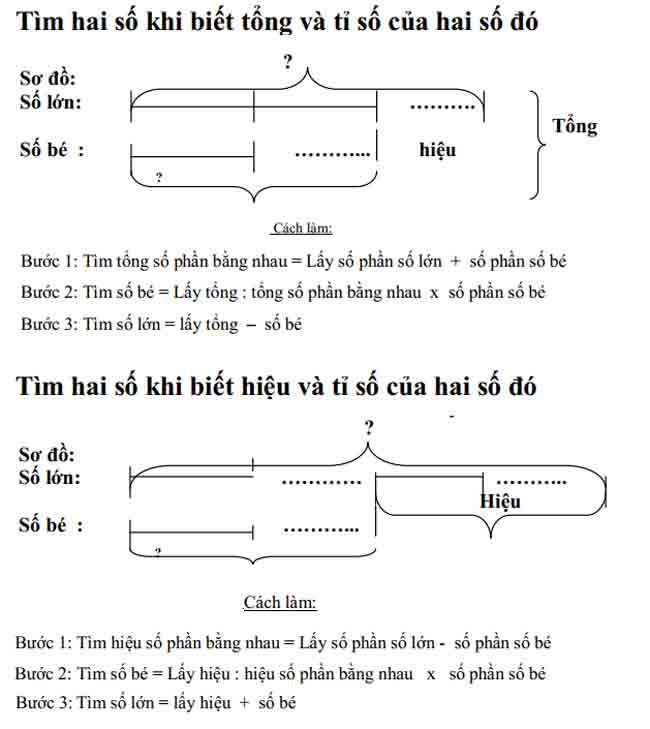
tìm hai số có tổng và tỷ số của chúng

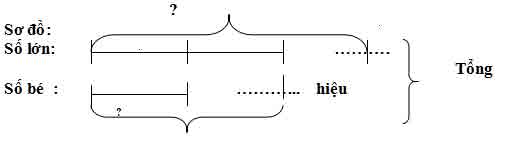
Cách làm:

bước 1: tìm tổng số phần bằng nhau = lấy số phần của số lớn + số phần của số bé

bước 2: tìm số nhỏ = tổng: tổng số phần bằng nhau × số phần của số nhỏ

bước 3: tìm số lớn = tổng – số nhỏ

tìm hai số có hiệu và tỷ số của chúng

Cách làm:

bước 1: tìm hiệu của các phần bằng nhau = lấy số phần của số lớn – số phần của số nhỏ

bước 2: tìm số nhỏ = lấy hiệu số: hiệu của các phần bằng nhau × số phần nhỏ

bước: tìm số lớn = lấy hiệu + số nhỏ

g. toán tỷ lệ

1. khái niệm: hai đại lượng tỉ lệ thuận khi một đại lượng tăng (hoặc giảm) nhiều lần thì đại lượng kia cũng tăng (hoặc giảm) nhiều lần.

2. Bài toán ví dụ: Một ô tô đi được quãng đường 90 km trong hai giờ. Hỏi ô tô đó đã đi được bao nhiêu km trong 4 giờ?

tóm tắt:

2 giờ: 90 km

4 giờ:… km?

giải pháp

phương pháp 1:

sau một giờ ô tô đi được:

90: 2 = 45 (km) (*)

Xem Thêm : mẫu đơn xin việc đánh máy

sau 4 giờ ô tô đi được:

45 × 4 = 180 (km)

câu trả lời: 180km

dạng 2:

4 giờ là 2 giờ số lần là:

4: 2 = 2 (lần) (**)

Xem Thêm : mẫu đơn xin việc đánh máy

sau 4 giờ ô tô đi được:

90 × 2 = 180 (km)

câu trả lời: 180km

(*) bước này là “giảm xuống đơn vị” (**) bước này là “tìm điểm”

h. tính toán tỷ lệ nghịch

1. Khái niệm: hai đại lượng tỉ lệ nghịch khi một đại lượng tăng (hoặc giảm) bao nhiêu lần thì đại lượng kia giảm (hoặc tăng).

2. Ví dụ: để hoàn thành việc xây dựng căn hộ trong hai ngày, cần 12 người. Hỏi bao nhiêu người xây được tầng đó trong 4 ngày? (mức độ công việc của mỗi người là như nhau)

tóm tắt:

2 ngày: 12 người

4 ngày:…. mọi người?

giải pháp

phương pháp 1:

bạn muốn hoàn thành việc xây dựng căn hộ sau 1 ngày, bạn cần số lượng người:

12 × 2 = 24 (người) (*)

Để hoàn thành phần móng trong 4 ngày, số người cần là:

24: 4 = 6 (người)

câu trả lời: 6 người

(*) bước này là bước “rút lại đơn vị”

dạng 2:

4 ngày là 2 ngày số lần là:

4: 2 = 2 (lần) (**)

Để hoàn thành phần móng trong 4 ngày, số người cần là:

12: 2 = 6 (người)

câu trả lời: 6 người

(**) bước này là bước “tìm điểm”

tôi. tìm các phân số của một số

kl: Bạn muốn tìm phân số của một số, hãy nhân số đó với phân số đã cho.

công thức chung: giá trị a / b của a = a × a / b

ví dụ: trong rổ có 12 quả cam. 2/3 số cam trong rổ là bao nhiêu?

giải pháp

2/3 số cam trong rổ là:

12 × 2/3 = 8 (quả)

câu trả lời: 8 kết quả

k. tìm một số có giá trị phân số đã biết

kl: Chúng ta muốn tìm một số khi chúng ta biết một giá trị phân số của số đó, chúng ta chia giá trị đó cho phân số.

cttq:

a / b giá trị của a = giá trị của phân số: a / b

ví dụ: đối với 2/3 số cam trong rổ cam thì 8. Trong rổ đó có bao nhiêu quả cam?

giải pháp

số quả cam trong rổ là:

8: 2/3 = 12 (quả)

ts: 12 kết quả

l. tỷ lệ phần trăm

1. tìm tỉ số phần trăm của hai số: ta làm như sau:

– tìm thương của hai số đó dưới dạng số thập phân.

– nhân thương số đó với 100 và thêm dấu phần trăm (%) vào bên phải của sản phẩm tìm được.

cttq: a: b = t (stp) = stp × 100 (%)

ví dụ: tìm tỷ lệ phần trăm của 315 và 600

giải pháp

phần trăm của 315 và 600 là:

315: 600 = 0,525 = 52,5%

cần thiết: 52,5%

2. tìm giá trị phần trăm của một số nhất định: chúng tôi chia số đó cho 100 và nhân với phần trăm hoặc nhân số đó với phần trăm rồi chia cho 100.

cttq: value% = number to: 100 × number of% hoặc value% = number of to × number of%: 100

p. vd: the school of pronouns có 600 học sinh. số học sinh nữ chiếm 45% số học sinh toàn trường. Tính số học sinh nữ của trường.

giải pháp

số học sinh của trường đó là:

600: 100 × 45 = 270 (sinh viên)

như: 270 sinh viên

3. tìm một số biết giá trị phần trăm của số đó: ta lấy giá trị phần trăm của số đó chia cho phần trăm rồi nhân với 100 hoặc lấy giá trị phần trăm của số đó nhân với 100 rồi chia cho phần trăm.

cttq: số a = giá trị%: số phần trăm × 100 hoặc số a = giá trị% × 100: số phần trăm

p. ví dụ: tìm một số có 30% là 72.

giải pháp

giá trị của số đó là:

72: 30 × 100 = 240

địa chỉ: 240

m. bảng đơn vị độ dài

1. bảng đơn vị độ dài :

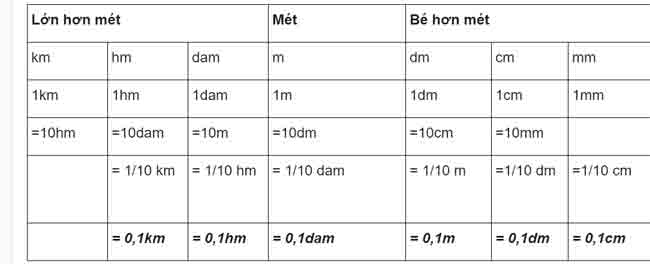
2. Nhận xét:

• hai đơn vị đo độ dài liên tiếp gấp 10 lần (hoặc nhỏ hơn) lần nhau.

ví dụ: 1m = 10dm

1 cm = 1/10 dm = 0,1 dm

• đơn vị đo độ dài của một chữ số.

ví dụ: 1245m = 1km 2hm 4dam 5m

n. bảng đơn vị đo lường

1. bảng đơn vị đo lường:

2. Nhận xét:

• hai đơn vị khối lượng liên tiếp gấp 10 lần (hoặc nhỏ hơn) nhau.

p. ví dụ: 1kg = 10hg

1 g = 1/10 ngày = 0,1 ngày

• một chữ số cho mỗi đơn vị khối lượng.

p. ví dụ: 1245 g = 1 kg 2 kg 4 ngày 5 g

o. bảng đơn vị đo diện tích

1. bảng đơn vị đo diện tích:

2. Nhận xét:

• hai đơn vị diện tích liền kề gấp 100 lần (hoặc nhỏ hơn) lần nhau.

ví dụ: 1m2 = 100 dm2

1 cm2 = 1/100 dm2 = 0,01 dm2

• đơn vị độ dài có hai chữ số.

ví dụ: 1245m2 = 12dam2 45m2

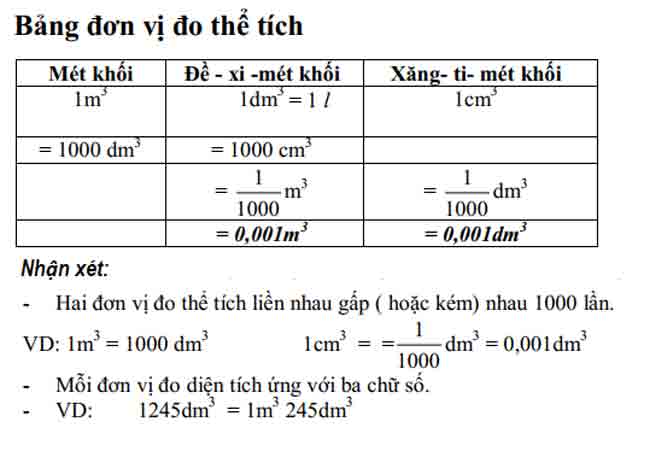
p. bảng đơn vị âm lượng

nhận x đặt:

• hai đơn vị âm lượng liền kề gấp 1000 lần (hoặc nhỏ hơn) nhau.

ví dụ: 1m3 = 1000 dm3

1 cm3 = 1/1000 dm3 = 0,001 dm3

• mỗi đơn vị diện tích có ba chữ số.
• ví dụ: 1245dm3 = 1m3 245dm3

ghi chú : 1dm3 = 1 l

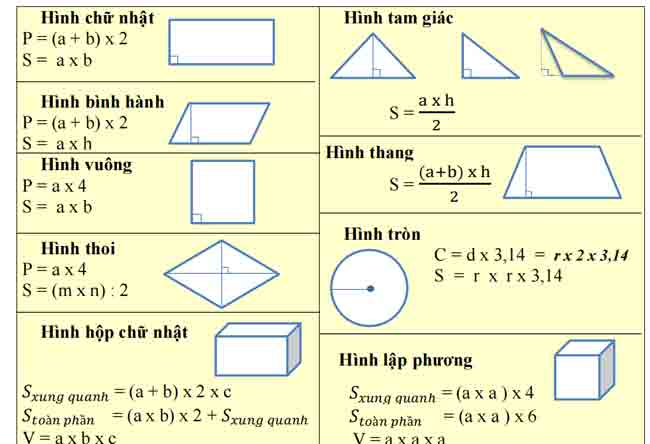
r. hình vuông

1. tính chất: hình vuông là hình tứ giác có 4 góc vuông và 4 cạnh có độ dài bằng nhau.

tiếp theo được ký hiệu bằng

2. tính chu vi: để tính chu vi hình vuông, chúng ta nhân số đo của một cạnh với 4.

cttq: p = a × 4

Để tìm một cạnh của hình vuông, chúng ta chia chu vi cho 4. a = p: 4

3. tính diện tích : Để tính diện tích hình vuông, chúng ta nhân số đo của một cạnh với chính nó.

cttq: s = a × a

· muốn tìm một cạnh của hình vuông, chúng ta tìm nếu một số nhân với chính nó bằng diện tích thì đó là cạnh.

· ví dụ: cho một diện tích hình vuông là 25 m2. tìm cạnh của hình vuông đó.

giải pháp

chúng ta có 25 = 5 × 5; vậy cạnh của hình vuông là 5m

s. hình chữ nhật

1. tính chất: hình chữ nhật là hình tứ giác có 4 góc vuông, 2 chiều dài bằng nhau, 2 chiều rộng bằng nhau.

chiều dài là a, chiều rộng là b

2. tính chu vi : để tính chu vi hình chữ nhật ta thêm số đo chiều dài cộng số đo chiều rộng

(cùng một đơn vị) rồi nhân với 2.

cttq: p = (a + b) × 2

* muốn tìm chiều dài ta chia chu vi cho 2 rồi trừ chiều rộng a = p: 2 – b

· chúng ta muốn tìm chiều rộng, chúng ta chia chu vi cho 2 và sau đó trừ chiều dài.

b = p: 2 – a

3. tính diện tích : để tính diện tích hình chữ nhật, ta lấy số đo chiều dài nhân với số đo chiều rộng (cùng một đơn vị).

cttq: s = a × b

· Để tìm chiều dài, chúng ta chia diện tích cho chiều rộng. a = s: b

· muốn tìm chiều rộng, chúng ta chia diện tích cho chiều dài.

b = s: a

t. hình bình hành

thuộc tính : hình bình hành có hai cặp

Các cạnh đối diện song song và bằng nhau.

ký hiệu

: dưới cùng là a,

chiều cao là h

tính chu vi : chu vi hình bình hành là tổng độ dài của 4 cạnh

tính diện tích : để tính diện tích hình bình hành, chúng ta nhân chiều dài của đáy với chiều cao (cùng một đơn vị)

cttq : s = a × h

– chúng tôi muốn tìm chiều dài của cơ sở , chúng tôi lấy diện tích chia cho chiều cao.

a = s: b

– chúng tôi muốn tìm chiều rộng , chúng tôi lấy diện tích chia cho chiều dài.

b = s: a

u. hình thoi

thuộc tính :

một hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau

Một hình thoi có hai đường chéo vuông góc với nhau và gặp nhau tại trung điểm của mỗi đường.

hai đường chéo là m và n

tính chu vi : để tính chu vi hình thoi, chúng ta nhân số đo của một cạnh với 4.

tính diện tích : diện tích hình thoi bằng tích độ dài hai đường chéo chia cho 2 (cùng đơn vị).

v. hình thang

thuộc tính : hình thang có một cặp cạnh đối diện song song.

– height: là đoạn thẳng giữa hai đáy và vuông góc với hai đáy .

ký hiệu: đáy lớn là a , đáy nhỏ là b, chiều cao là h

Tính diện tích : Để tính diện tích hình thang, ta lấy tổng độ dài của hai đáy nhân với chiều cao (cùng đơn vị) rồi chia cho 2.

s = (a + b) × h: 2

hoặc: Để tính diện tích hình thang, chúng tôi lấy giá trị trung bình của hai đáy nhân với chiều cao.

s = × h

Xem Thêm : Cách viết sơ yếu lý lịch học sinh sinh viên

– chúng tôi cộng hai cơ số: chúng tôi lấy diện tích nhân với 2 rồi chia cho chiều cao.

(a + b) = s × 2: h

– tính trung bình của hai cơ sở: chúng tôi lấy diện tích chia cho chiều cao.

= s: h

– tính chiều dài của cơ sở lớn: chúng tôi lấy diện tích nhân với 2, chia cho chiều cao và sau đó trừ chiều dài của cơ sở nhỏ.

a = s × 2: h – b

– tính chiều dài của cơ sở nhỏ: chúng tôi lấy diện tích nhân với 2, chia cho chiều cao và sau đó trừ chiều dài của cơ sở lớn.

b = s × 2: h – a

– tính chiều cao: chúng tôi lấy diện tích nhân với 2 rồi chia cho tổng độ dài của hai cơ sở.

h = s × 2: (a + b)

hoặc: tính chiều cao: chúng tôi lấy diện tích chia cho giá trị trung bình của hai cơ sở.

x. hình tam giác

thuộc tính : tam giác có ba cạnh, ba góc, ba đỉnh.

chiều cao là đoạn thẳng từ đỉnh vuông góc đến cạnh đối diện.

ký hiệu dưới cùng là a , chiều cao là h

tính chu vi : chu vi hình tam giác là tổng độ dài của 3 cạnh.

tính diện tích : Để tính diện tích hình tam giác, chúng ta lấy chiều dài của đáy nhân với chiều cao (cùng một đơn vị) rồi chia cho 2.

s = a × h: 2

– tính đường viền dưới cùng: chúng tôi lấy diện tích nhân với 2 rồi chia cho chiều cao.

a = s × 2: h

– tính chiều cao: chúng tôi lấy diện tích nhân với 2 rồi chia cho cạnh dưới.

h = s × 2: a

y. vòng tròn

1. thuộc tính : hình tròn với tất cả các bán kính bằng nhau.

– đường bao quanh vòng tròn được gọi là đường tròn.

– điểm chính giữa của vòng tròn là tâm.

– đoạn thẳng nối tâm với một điểm trên đường tròn được gọi là bán kính. biểu tượng là r

– đường thẳng đi qua tâm và nối hai điểm của đường tròn được gọi là đường kính.

Đường kính gấp đôi bán kính. ký hiệu là d

2. tính chu vi : để tính chu vi hình tròn, ta nhân đường kính với 3,14.

c = d × 3,14

hoặc nhân bán kính với 2 và nhân với 3,14.

c = r × 2 × 3,14 p>

tính đường kính: chúng ta chia chu vi cho 3,14

d = c: 3,14

tính bán kính: chúng ta chia chu vi cho 2 rồi chia cho 3,14

r = c: 2: 3,14 (tính nháp: r = c: 6,28)

3. tính diện tích : Để tính diện tích hình tròn, ta lấy bán kính nhân với bán kính rồi nhân với 3,14. s = r × r × 3,14

– biết diện tích , muốn tìm bán kính ta làm như sau: chia diện tích cho số 3,14 để tìm tích của hai bán kính và sau đó chúng tôi tìm xem một số nhân với chính nó có bằng tích đó hay không, vì vậy đó là bán kính của hình tròn.

ví dụ: Cho diện tích hình tròn bằng 28,26 cm2. tìm bán kính của hình tròn đó.

giải pháp

tích của hai bán kính hình tròn là:

28,26: 3,14 = 9 (cm2)

vì 9 = 3 × 3, bán kính của hình tròn là 3 cm

hình hộp chữ nhật

1. thuộc tính : hình hộp chữ nhật có 6 mặt, hai mặt dưới và bốn cạnh.

– có 8 đỉnh, 12 cạnh

– có ba kích thước: chiều dài ( a) , chiều rộng ( b ), chiều cao ( c ).

2. tính diện tích x xung quanh: để tính diện tích xung quanh một hình hộp chữ nhật, ta lấy chu vi của đáy nhân với chiều cao (cùng một đơn vị đo) .

s × q = p (xuống) × c p>

o: s × q = (a + b) × 2 > × c

– chúng tôi muốn tìm chu vi đáy , chúng tôi chia diện tích xung quanh cho chiều cao.

p (xuống) = s × q: c

– chúng tôi muốn tìm chiều cao , chúng tôi chia diện tích xung quanh cho chu vi đáy

c = s × q: p (bottom)

– chúng tôi muốn tìm tổng của hai cơ số , chúng tôi lấy diện tích xung quanh chia cho 2 rồi chia cho chiều cao.

(a + b) = s × q: 2: h

– chúng tôi muốn tìm chiều dài , chúng tôi lấy diện tích xung quanh chia cho 2, chia cho chiều cao, sau đó trừ chiều rộng.

a = s × q: 2: c – b

– chúng tôi muốn tìm chiều rộng , chúng tôi lấy diện tích xung quanh chia cho 2, chia cho chiều cao, sau đó trừ chiều dài.

b = s × q: 2: c – a

– tính tổng diện tích: Để tính tổng diện tích của một hình hộp chữ nhật, chúng ta lấy diện tích xung quanh nó cộng với diện tích của hai đáy.

stp = s × q + s (2 bên dưới)

hoặc: stp = (a + b) × 2 × c + a × b × 2

– muốn tìm diện tích cơ sở chúng tôi lấy chiều dài nhân với chiều rộng.

s (xuống) = a × b

– chúng tôi muốn tìm chiều dài, chúng tôi lấy diện tích của đáy chia cho chiều rộng .

a = s (xuống): b

– chúng tôi muốn tìm chiều rộng, chúng tôi lấy diện tích của cơ sở chia cho chiều dài.

b = s (dưới cùng): a

4. tính thể tích của hình hộp chữ nhật: ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo).

v = a × b × c

– chúng tôi muốn tìm chiều dài, chúng tôi lấy thể tích chia cho chiều rộng rồi chia cho chiều cao .

a = v: b: c

– chúng tôi muốn tìm chiều rộng, chúng tôi lấy thể tích chia cho chiều dài rồi chia cho chiều cao.

b = v: a: c

– chúng tôi muốn tìm chiều cao, chúng tôi lấy thể tích chia cho chiều dài rồi chia cho chiều rộng.

c = v: a: b

hoặc chia khối lượng cho diện tích của đế

c = v: s (dưới cùng)

khối lập phương

1. thuộc tính : một hình lập phương có 6 mặt là các hình vuông bằng nhau.

– có 8 đỉnh, 12 cạnh có độ dài bằng nhau. ký hiệu đường viền a

2. tính diện tích × xung quanh : chúng ta muốn tính diện tích × xung quanh khối lập phương mà chúng ta lấy

diện tích của một khuôn mặt nhân với 4: s × q = s (1 mặt) × > 4

3. tính tổng diện tích : để tính tổng diện tích của một hình lập phương, ta nhân diện tích một mặt với 6: stp = s (1 mặt) × 6

chúng tôi muốn tìm diện tích khuôn mặt chúng tôi lấy diện tích × đường viền chia cho 4 hoặc tổng diện tích chia cho 6.

s (1 bên) = s × q: 4

hoặc: s (1 bên) = stp: 6

– chúng tôi muốn tìm một cạnh của hình lập phương , chúng tôi tìm nếu một số nào đó nhân với chính nó bằng diện tích của một mặt thì đó chính là cạnh.

– vd : cho bề mặt 25 m2 một mặt. tìm cạnh của khối lập phương đó.

giải pháp

chúng tôi có 25 = 5 × 5;

khi đó cạnh của hình lập phương là 5m

4. tính thể tích của khối lập phương: chúng ta nhân cạnh với cạnh rồi với cạnh.

v = a × a × a

Tôi muốn tìm một cạnh của hình lập phương , chúng tôi tìm một số nhân với chính nó và sau đó nhân nó với thể tích, vì vậy đó là cạnh.

ví dụ: cho một thể tích 125 m2. tìm cạnh của khối lập phương đó.

giải pháp

chúng ta có 25 = 5 × 5 × 5; vậy cạnh của hình lập phương là 5m

toán chuyển động

i. có một động từ chuyển động

1. tốc độ: Để tính tốc độ, chúng tôi chia khoảng cách cho thời gian.

v = s: t

2. khoảng cách: để tính khoảng cách, nhân tốc độ với thời gian.

s = v × t

3. thời gian: để tính thời gian, chúng ta chia quãng đường cho tốc độ

t = s: v

II. Có hai động tử cùng chuyển động

1. cùng nhau x xuất phát ngược chiều nhau để gặp nhau:

a, tìm tổng vận tốc của hai chuyển động:

(v1 + v2) = s: t

b, tìm khoảng cách của hai lần di chuyển:

s = (v1 + v2) × t

c, tìm thời gian của hai lần di chuyển:

t = s: (v1 + v2)

2. cùng nhau x xuất phát cùng hướng gặp nhau:

a, tìm sự khác biệt về tốc độ của hai chuyển động: (v1 – v2) = s: t

b, tìm quãng đường của hai lần di chuyển: s = (v1 – v2) × t

c, tìm thời gian của hai lần chuyển động: t = s: (v1 – v2)

iii. chuyển động dưới nước

1. di chuyển x dòng cuối:

a. tìm vận tốc xuôi dòng:

v × tail = vboat + vagua = s: t

b. tìm khoảng cách:

s = (vship + máng) × t

c. tìm thời gian:

t = s: (thuyền + nước)

2. chuyển động ngược dòng:

a. tìm tốc độ ngược dòng:

reverse = vboat – vwater = s: t

b. tìm khoảng cách:

s = (vship – máng) × t

c. tìm thời gian:

t = s: (vship – vagua)