Bạn đang xem: ✅ Công thức tính lim ⭐️⭐️⭐️⭐️⭐️ Tại DongnaiArt

Giới hạn của hàm số, cách tính và bài tập áp dụng

giới hạn hữu hạn

Giới hạn vô cực, Giới hạn ở vô cực

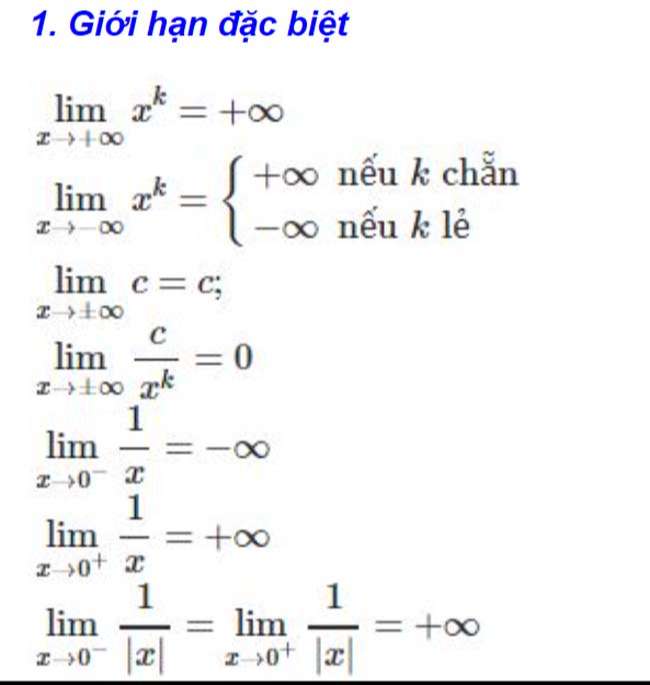
Giới hạn 1 bên

Bài tập áp dụng tìm giới hạn

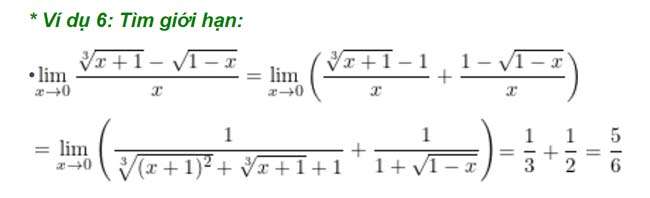
Ví dụ 8: Tìm giới hạn sau

Mối quan hệ giữa giới hạn một bên và giới hạn tại một điểm

Bảng các công thức tính giới hạn hàm số

một số phương pháp tính toán thủ công

tính toán giới hạn của một chuỗi

phương pháp 1: sử dụng định nghĩa tìm giới hạn 0 của một dãy

phương pháp 2: tìm giới hạn của một dãy số bằng công thức

một số công thức mà chúng ta thường tìm thấy khi tính giới hạn của một hàm như sau:

Công thức trên có thể biến tấu thành các dạng khác tuy nhiên về bản chất thì không thay đổi.

phương pháp 3: sử dụng định nghĩa tìm kiếm giới hạn hữu hạn

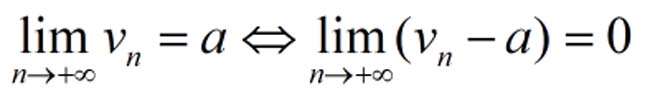
Cách 4: Sử dụng các giới hạn đặc biệt cùng với định lý để giải quyết các bài toán tìm giới hạn dãy số

• chúng tôi thường sử dụng biểu mẫu hạn chế:

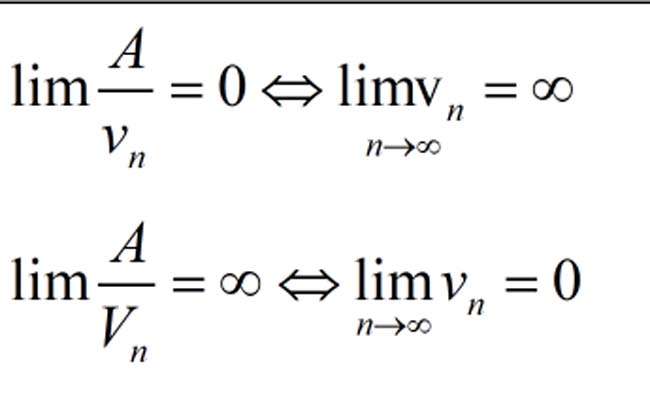
• Nếu biểu thức có dạng phân thức tử số và mẫu số chứa lũy thừa của n thì ta tiến hành chia cả tử và mẫu cho n^k với k là mũ cao nhất ở bậc mẫu.
• Nếu biểu thức chứa căn thức cần nhân một lượng liên hợp để đưa về dạng cơ bản thì ta có một số lượng liên hợp cần thiết như sau:

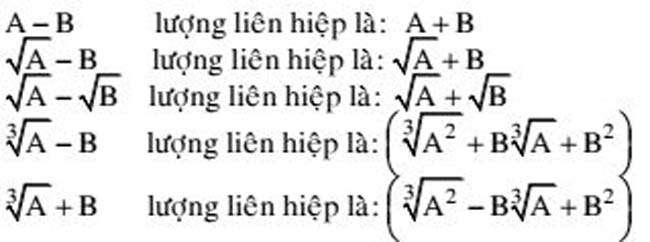
Cách 5: Áp dụng công thức tính tổng cấp số nhân lùi vô hạn, tính giới hạn, biểu thị một số thập phân vô hạn tuần hoàn thành phân số.

• cấp số nhân vô hạn lùi là cấp số nhân vô hạn và có cấp số nhân là | q | & lt; 1
• tổng các số hạng của một cấp số nhân lùi vô hạn (un)

s = u1 + u2 + u3 + u4 +…. + a = u1 / (1 – q)

• tất cả các số thập phân được biểu thị dưới dạng lũy ​​thừa của 10.

Câu 6: Tìm giới hạn vô hạn của dãy số theo định nghĩa

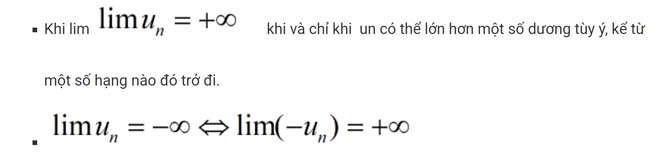
Cách 7: Tìm giới hạn của một dày số bằng cách sử dụng định lý, quy tắc tìm giới hạn vô cực

thử một chuỗi giới hạn

áp dụng định lý kỷ lục địa lý:

• nếu dãy (un) tăng và bị giới hạn ở trên, nó có giới hạn.
• nếu dãy (un) giảm và bị giới hạn ở dưới, nó có giới hạn.

gia số và giới hạn thử nghiệm:

chứng minh rằng một dãy số tăng và có giới hạn trên (giới hạn tăng và giảm) bởi số m ta thực hiện: tính các số hạng đầu tiên của dãy số và quan sát mối quan hệ để dự đoán chiều tăng (chiều giảm) và số của m.

Để tính giới hạn của một dãy số, chúng tôi thực hiện một trong hai phương pháp sau:

Xem Thêm : Cách đổi tiền Trung Quốc sang Việt Nam cho du học sinh

phương pháp 1

đặt lim a = a. Từ lim u (n + 1) = lim f (un), chúng ta nhận được một phương trình ẩn a.

giải phương trình để tìm một nghiệm của a và giới hạn của dãy số (un) là một trong các nghiệm của phương trình. nếu phương trình có nghiệm duy nhất thì đó là giới hạn của dãy số cần tìm. và nếu phương trình có nhiều hơn một nghiệm thì dựa vào tính chất của dãy số để loại bỏ nghiệm.

lưu ý: ranh giới trình tự, nếu có, là duy nhất.

phương pháp 2: tìm công thức chung của một dãy số bằng cách đưa ra dự đoán. chứng minh công thức tổng quát a bằng quy nạp toán học. tính giới hạn của dãy số thông qua công thức chung đó.

tính toán giới hạn hàm

Để tính giới hạn của hàm chúng ta có thể thực hiện một số phương pháp như sau:

• sử dụng định nghĩa để tìm giới hạn
• tìm giới hạn của hàm bằng công thức
• sử dụng định nghĩa để tìm giới hạn một phía
• sử dụng định lý và công thức để tìm giới hạn một phía
• tính giới hạn vô cùng
• tìm giới hạn của một hàm có dạng 0/0
• hình thức không xác định

đây là một số công thức rất cơ bản để tính toán các hàm:

Cách tính lim bằng máy tính

bước 1: trước tiên hãy nhập biểu thức vào máy tính

bước 2: sử dụng hàm gán số để tính giá trị biểu thức

Bước 3: Chú ý đến việc gán các giá trị sau:

+) lim đến dương vô cùng, sau đó gán số 100000

+) lim đến âm vô cùng, sau đó gán số -100000

+) giới hạn thành 0, sau đó chỉ định số 0,00000001

+) giới hạn ở bất kỳ số nào như +3 bản đồ đến 3.000000001 và 3 bản đồ là 2.9999999999

Giải tích lim là một dạng bài tập khá cơ bản nhưng vẫn chiếm một vài câu trong đề thi THPT quốc gia. bạn cần đảm bảo độ chính xác khi làm như vậy. đặc biệt bạn có thể sử dụng máy tính casio để có thể tính toán nhanh hơn và chính xác hơn.

chủ đề giới hạn và liên tục

cách tính giới hạn của hàm?

tính toán giới hạn của các chức năng đã xác định

nếu hàm f (x) được xác định tại điểm giới hạn. vì vậy chúng ta chỉ cần thay dấu chấm đó trong biểu thức bên dưới dấu giới hạn để nhận được kết quả mà chúng ta đang tìm kiếm.

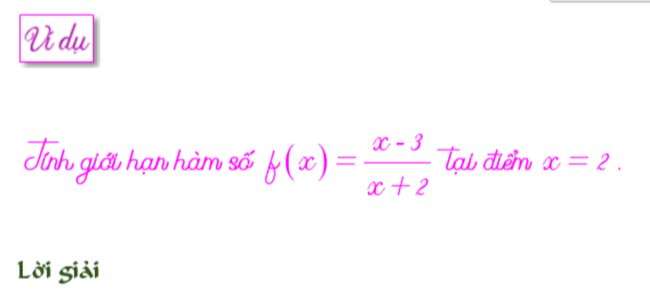
Ta chỉ việc thay x=2 vào biểu thức trong dấu lim ta được -1/4. Và đó chính là kết quả của giới hạn trên.

tìm giới hạn của các hàm có định dạng giống hệt nhau

Xem Thêm : Đề thi Đường lối cách mạng Đảng CSVN – Có đáp án

đối với dạng không xác định, chúng tôi quan tâm đến một số dạng phổ biến như sau:

1. tìm giới hạn của một hàm có dạng 0 trên 0

đối với dạng 0 trên 0, chúng tôi chia nó thành 2 loại: loại có giới hạn không chứa gốc và loại có chứa gốc.

loại căn bao gồm các loại giới hạn và phân số đặc biệt trong đó tử số và mẫu số là đa thức.

giới hạn đặc biệt của dạng 0 trên 0 được đề cập trong chương trình phổ biến hiện tại là:

cách tính giới hạn của dạng 0 tại 0 của đa thức qua đa thức, chúng ta có thể tính giới hạn của nó bằng cách sử dụng sơ đồ hocner.

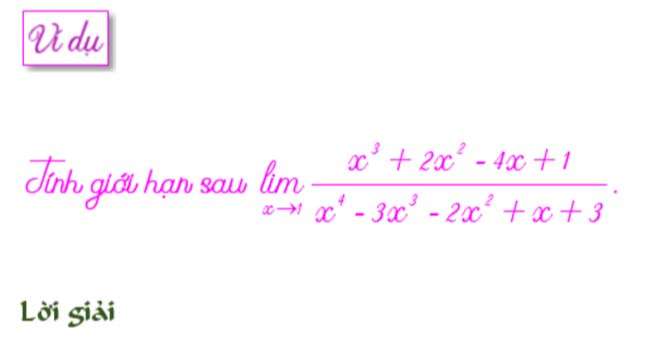
Ta thấy x=1 là nghiệm của cả tử số và mẫu số. Ta dùng lược đồ Hoocner để phân tích tử số và mẫu số.

Còn để tính loại chứa căn ta thực hiện nhân cả tử và mẫu với biểu thức liên hợp.

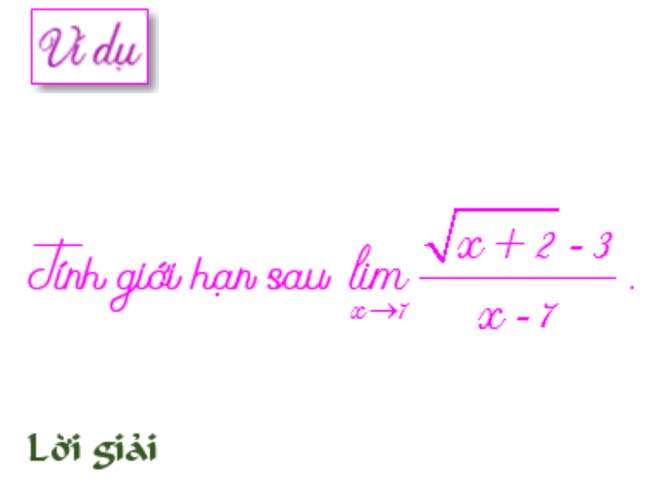
Với căn bậc 3 ta cũng làm tương tự.

Ta có:

Trong trường hợp giới hạn có căn bậc hai và căn bậc hai, ta cộng và trừ 1 lượng để thu được tổng hiệu của hai giới hạn có dạng 0 trên 0.

GIỚI HẠN DẠNG VÔ CÙNG TRÊN VÔ CÙNG

Đối với dạng giới hạn ở vô cùng trên vô cùng, chúng ta giải quyết bằng cách chia cả tử số và mẫu số cho x với số mũ cao nhất của tử số hoặc mẫu số. lưu ý dạng này vì x tiến tới âm vô cùng, chúng ta thường nhầm lẫn về dấu. cụ thể, khi đặt x vào căn bậc hai, chúng ta phải bỏ dấu -.

GIỚI HẠN DẠNG VÔ CÙNG TRỪ VÔ CÙNG

với dạng ẩn vô cực (vô cực trừ vô cực) ta thực hiện bằng hai phương pháp: nhóm ẩn bậc cao hoặc phép nhân liên hợp. còn cách nào tốt hơn để tiếp tục.

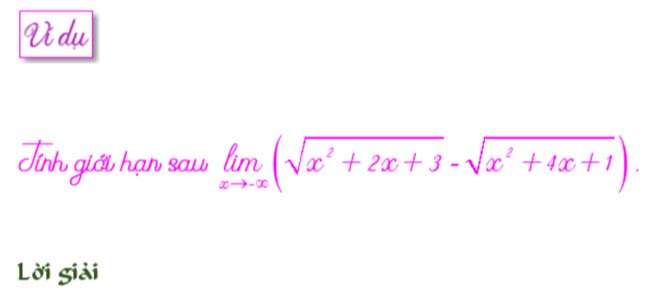
Trường hợp này chúng ta cần nhân liên hợp bởi vì nếu nhóm x thì sẽ lại đưa về dạng bất định 0 nhân vô cùng.

Bài này giống bài trên đều là dạng vô cùng trừ vô cùng. Nhưng ta lại để ý là hệ số bậc cao nhất trong 2 căn là khác nhau. Vì vậy bài này chúng ta nên nhóm nhân tử chung.

1m × định dạng không giới hạn

với giới hạn từ dạng 1 đến vô hạn, chúng tôi tính toán qua giới hạn đặc biệt sau:

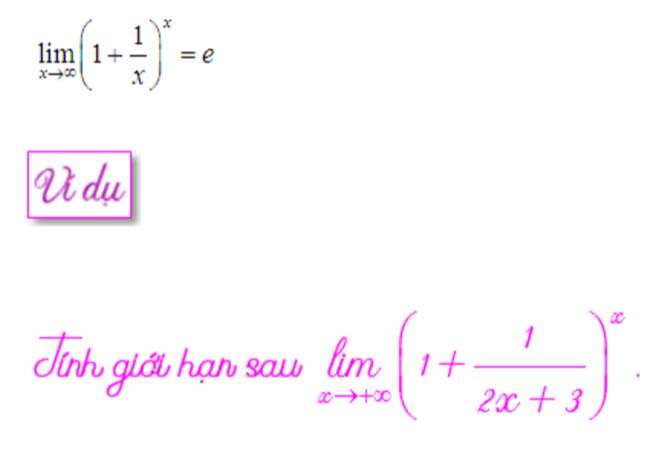
GIỚI HẠN DẠNG 0 NHÂN VÔ CÙNG

Về bản chất, giới hạn của dạng 0 nhân với vô cùng có thể được rút gọn thành dạng 0 trên 0 hoặc dạng vô cùng trên vô cùng thông qua một số phép biến đổi như được chỉ ra ở đầu bài viết này trong định nghĩa. với dạng giới hạn này ta phải biến đổi về dạng xác định hoặc các dạng giới hạn không xác định đã nêu ở trên. tùy từng mặt hàng cụ thể mà chúng ta nên thay đổi cho phù hợp.

Phân dạng và các phương pháp giải toán chuyên đề giới hạn

bài tập 1. giới hạn của dãy số . loại 1. sử dụng định nghĩa để tìm giới hạn 0 của dãy số loại 2. sử dụng định lý để tìm giới hạn 0 của dãy số thuộc loại 3. sử dụng định lý và giới hạn đặc biệt để giải các bài toán về dãy giới hạn dạng 4. sử dụng công thức tính tổng của một cấp số nhân vô hạn tuần hoàn, tìm giới hạn, biểu thị một số thập phân vô hạn tuần hoàn các phân số dạng 5. tìm giới hạn của vô cực của dãy bằng cách sử dụng định nghĩa dạng 6. tìm giới hạn của dãy bằng định lý giới hạn vô cùng của một số toán cao cấp {tham khảo} bài 2. giới hạn của hàm số dạng 1. sử dụng định nghĩa để tìm giới hạn dạng 2. tìm giới hạn của hàm số bằng công thức dạng 3. sử dụng định nghĩa để tìm giới hạn một phía của dạng 4. sử dụng định lý và công thức để tìm giới hạn một phía của dạng. 5. tìm giới hạn vô cực của dạng 6 tìm giới hạn của hàm số vô nghiệm dạng 0/0 dạng 7. dạng không xác định 8. dạng vô nghiệm một số toán cao cấp {tham khảo} bài 3. hàm số liên tục dạng 1. xét tính liên tục của hàm số f (x) tại điểm x0 có dạng 2. xét tính liên tục của hàm số tại một điểm có dạng 3. xét tính liên tục của hàm số trên một khoảng k thuộc dạng 4. tìm tính gián đoạn của hàm số f (x) dạng 5. chứng minh phương trình f (x) = 0 có nghiệm Một số bài tập lý thuyết {tham khảo}