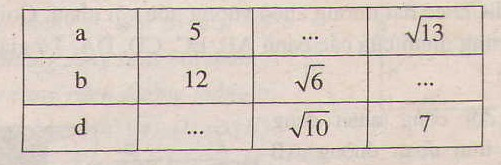Cùng xem Giải bài 58, 59, 60, 61, 62 trang 99 sgk toán 8 tập 1 – Giaibaitap.me trên youtube.
bài 58 trang 99 SGK Toán 8 tập 1
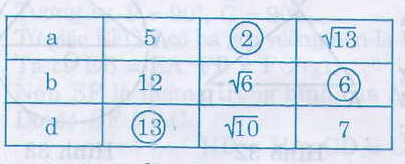
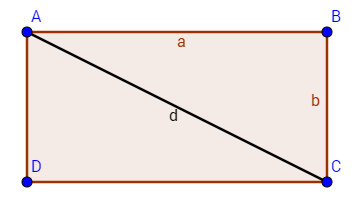
Điền vào chỗ trống biết \(a,b\) là độ dài cạnh, \(d\) là độ dài đường chéo của hình chữ nhật.
Giải pháp:
Cột thứ hai:
Áp dụng định lý Pitago cho tam giác vuông \(abc\) ta có:
\({d^{2}} = {\rm{ }}{a^2} + {\rm{ }}{b^2} = {\rm{ }}{5^ 2} + {\rm{ }}{12^2} = {\rm{ }}25{\rm{ }} + {\rm{ }}144{\rm{ }} = { rm{ }}169\)
Phải là \(d =\sqrt{169}= 13\)
Cột thứ ba:
Áp dụng định lý Pitago cho tam giác vuông \(abc\) ta có:
\({a^2} + {\rm{ }}{b^{2}} = {d^2} \rightarrow {a^2} = {\rm{ }}{d ^2} – {b^2} = (\sqrt{10}\))2 – (\(\sqrt{6}\))2
\(= 10 – 6 = 4\rightarrow a = \sqrt 4=2\)
Cột thứ tư:
Áp dụng định lý Pitago cho tam giác vuông \(abc\) ta có:
\({a^2} + {\rm{ }}{b^{2}} = {\rm{ }}{d^2} \rightarrow {b^2} = { rm{ }}{d^2} – {\rm{ }}{a^2} = {\rm{ }}{7^2} – (\sqrt{13}\))2
\(= 49 – 13 = 36\)\(\rightarrow b=\sqrt {36}= 6\)
Xem Thêm : Giải mã hiện tượng khí hư đặc dính cho chị em phụ nữ
Bài 59 Trang 99 SGK Toán 8 Tập 1
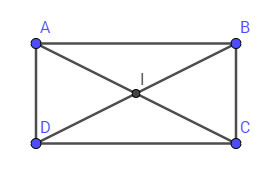
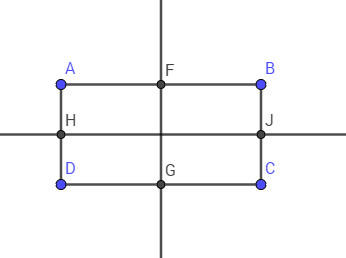
Chứng minh: a) Giao điểm của hai đường chéo của một hình chữ nhật là tâm đối xứng của hình chữ nhật đó.
b) Hai đường thẳng đi qua trung điểm của hai cặp cạnh đối diện của một hình chữ nhật là hai trục đối xứng của hình chữ nhật đó.
Giải pháp thay thế:
a) 
Vì hình bình hành lấy giao điểm của hai đường chéo làm tâm đối xứng và hình chữ nhật là hình bình hành nên giao điểm hai đường chéo của hình chữ nhật là tâm đối xứng của hình.
hai)
Vì hình thang cân là đường thẳng đi qua trung điểm của hai đáy là trục đối xứng và hình chữ nhật là hình thang cân có hai đáy là hai cạnh đối xứng của hình chữ nhật nên hai đường thẳng đó đi qua qua hai cặp cạnh của hình chữ nhật. Trung điểm của các cạnh là hai trục đối xứng của hình chữ nhật
bài 60 trang 99 SGK Toán 8 tập 1
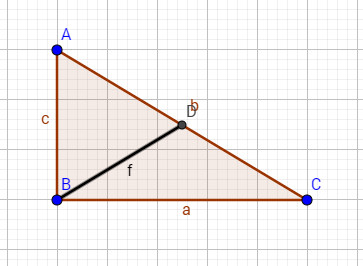
Tính độ dài từ trung tuyến đến cạnh huyền của một tam giác vuông có các góc vuông là \(7cm\) và \(24cm\).
Giải pháp thay thế:
Người ta gọi \(b\) là độ dài cạnh huyền của tam giác vuông \(abc\).
Theo định lý Pitago ta có:
\(\eqalign{ & {b^2} = {7^2} + {24^2} = 49 + 576 = 625 \cr & b = \sqrt {625} = 25 \cr} \)
Đường trung tuyến ứng với cạnh huyền bằng một nửa độ dài của cạnh huyền. Vậy trung tuyến của cạnh huyền là \(12,5cm\).
Bài 61 Trang 99 SGK Toán 8 Tập 1
Xem Thêm : Đàn Guitar Yamaha – Nhạc cụ Tiến Đạt
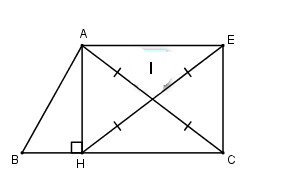
Cho tam giác \(abc\), chiều cao \(ah\). Gọi \(i\) là trung điểm của \(ac, e\), điểm đối xứng với \(h\) với \(i\). Tứ giác \(ahce\) là gì? Tại sao? Giải pháp:
Giả sử \(i\) là trung điểm của \(ac\) nên \(ia = ic\)\(e\) là điểm đối xứng với \ (h ) đến \(i\) nên \(i\) là trung điểm của \(he\) hoặc \(ie = ih\)
Tứ giác \(ahce\) có hai đường chéo cắt nhau tại trung điểm mỗi cạnh nên là hình bình hành (theo dấu hiệu 5)
Nếu không thì \(ah\) là đường cao nên \(\widehat{ahc}=90^0\)
Vậy \(ahce\) là hình chữ nhật (theo mã định danh 3)
bài 62 trang 99 SGK Toán 8 tập 1
Câu sau đây đúng hay sai?
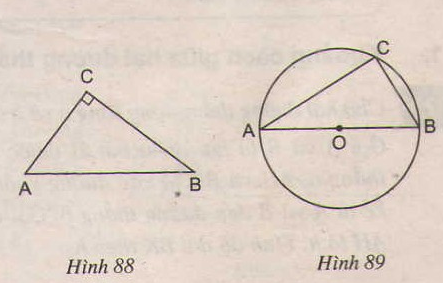
a) Nếu tam giác abc vuông góc với c thì điểm c nằm trên đường tròn đường kính ab(h.88)
b) Nếu điểm c nằm trên đường tròn đường kính ab (c khác a và b) thì tam giác abc vuông tại c(h.89).
Giải pháp
a) Đúng.
Gọi o là trung điểm của ab. Ta có co là trung tuyến ứng với cạnh huyền nên
\(oc = \frac{1}{2}ab\) hoặc \(oc = oa = ob\). Vậy a, b, c cùng thuộc một đường tròn bán kính oa. Vậy c thuộc đường tròn đường kính ab.
b) Đúng.
Gọi là tâm đường tròn. Đường trung tuyến của tam giác abc bằng nửa cạnh ab (do \(co = ao = ob\) ) nên tam giác abc vuông góc với c.
giaibaitap.me
Nguồn: https://dongnaiart.edu.vn
Danh mục: Tin tức
Lời kết: Trên đây là bài viết Giải bài 58, 59, 60, 61, 62 trang 99 sgk toán 8 tập 1 – Giaibaitap.me. Hy vọng với bài viết này bạn có thể giúp ích cho bạn trong cuộc sống, hãy cùng đọc và theo dõi những bài viết hay của chúng tôi hàng ngày trên website: Dongnaiart.edu.vn
