Cùng xem Giải bài 1, 2, 3, 4, 5 trang 91, 92 Sách giáo khoa Hình học 11 trên youtube.
Bài tập 1 trang 91 SGK hình học
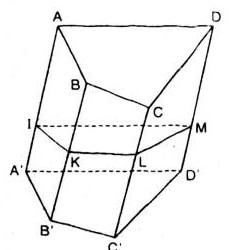
Đối với lăng trụ vuông: \(abcd.a’b’c’d’\). Mặt phẳng \((p)\) cắt các cạnh \(aa’, bb’, cc’, dd’\) tại \(i, k, l, m, tương ứng. ). Xét một vectơ có điểm đầu là \(i, k, l, m\) và có điểm cuối là một đỉnh của lăng trụ. Vui lòng chỉ định một vectơ:
a) một vectơ cùng hướng với \(\overrightarrow{ia}\);
b) một vectơ cùng hướng với \(\overrightarrow{ia}\);
c) Một vectơ ngược hướng với \(\overrightarrow{ia}\).
Người chiến thắng.
a) Các vectơ cùng hướng với \(\overrightarrow{ia}\) là: \(\overrightarrow{ia’}\), \(\overrightarrow{kb} ), \(\overrightarrow{kb’}\), \(\overrightarrow{lc}\), \(\overrightarrow{lc’}\), \( overrightarrow{md}\), \(\overrightarrow{md’}\).
b) Các vectơ cùng hướng với \(\overrightarrow{ia}\) là: \(\overrightarrow{kb}\), \(\overrightarrow{lc}\ ) , \(\overrightarrow{md}\).
c) Vectơ ngược hướng với \(\overrightarrow{ia}\) là: \(\overrightarrow{ia’}\), \(\overrightarrow{kb ‘} \), \(\overrightarrow{lc’}\), \(\overrightarrow{md’}\).
bài giảng 2 trang 91 SGK Hình học
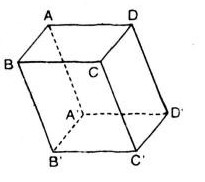
Đối với hình hộp \(abcd.a’b’c’d’\). Bằng chứng:
a) \(\overrightarrow{ab}\) + \(\overrightarrow{b’c’}\) + \(\overrightarrow{dd’}\) = \(\overrightarrow{ac’}\);
b) \(\overrightarrow{bd}\) – \(\overrightarrow{d’d}\) – \(\overrightarrow{b’d’}\ ) = \(\overrightarrow{bb’}\);
c) \(\overrightarrow{ac}\) + \(\overrightarrow{ba’}\) + \(\overrightarrow{db}\) + \( overrightarrow{c’d}\) = \(\overrightarrow{0}\).
NGƯỜI CHIẾN THẮNG
a) \(\overrightarrow{ab}\) + \(\overrightarrow{b’c’}\) + \(\overrightarrow{dd’}\) = \(\overrightarrow{ab}\) + \(\overrightarrow{bc}\) + \(\overrightarrow{cc’}\) = \(\overrightarrow{ac ‘}\);
b) \(\overrightarrow{bd}\) – \(\overrightarrow{d’d}\) – \(\overrightarrow{b’d’}\ ) = \(\overrightarrow{bd}\) + \(\overrightarrow{dd’}\) + \(\overrightarrow{d’b’}\) = \ (\overrightarrow{bb’}\);
c) \(\overrightarrow{ac}\) + \(\overrightarrow{ba’}\) + \(\overrightarrow{db}\) + \( overrightarrow{c’d}\) = \(\overrightarrow{ac}\) + \(\overrightarrow{cd’}\) + \(\overrightarrow{d’ b’}\) + \(\overrightarrow{b’a}\) = \(\overrightarrow{0}\).
Bài 3 Trang 91 SGK Hình học 11
đại diện cho hình bình hành \(abcd\). Cho \(s\) là một điểm nằm ngoài mặt phẳng chứa hình bình hành. Chứng minh: \(\overrightarrow{sa}\) + \(\overrightarrow{sc}\) = \(\overrightarrow{sb}\) + \(\overrightarrow{sd } \).
NGƯỜI CHIẾN THẮNG
Gọi \(o\) là tâm của hình bình hành \(abcd\). Sau đó:
\(\left.\begin{matrix}\overrightarrow{sa} +\overrightarrow{sc}= 2\overrightarrow{so}\\ \overrightarrow{sb}+\ overrightarrow{sd}=2\overrightarrow{so} \end{matrix}\right\}\leftrightarrow \overrightarrow{sa}+\overrightarrow{sc}=\overrightarrow{sb}+\ overrightarrow{sd}.\)
Bài 4 Trang 92 SGK Hình học 11
Cho tứ diện \(abcd\). Gọi \(m\) và \(n\) lần lượt là trung điểm của \(ab\) và \(cd\). Bằng chứng:
a) \(\overrightarrow{mn}=\frac{1}{2}\left ( \overrightarrow{ad}+\overrightarrow{bc} \right );\)
b) \(\overrightarrow{mn}=\frac{1}{2}\left ( \overrightarrow{ac}+\overrightarrow{bd} \right ).\)
NGƯỜI CHIẾN THẮNG
(Hình 33)
a) \(\overrightarrow{mn}=\overrightarrow{ma}+\overrightarrow{ad}+\overrightarrow{dn}.\)
Xem Thêm : Soạn bài Vợ nhặt | Ngắn nhất Soạn văn 12 – VietJack.com
\(\overrightarrow{mn}=\overrightarrow{mb}+\overrightarrow{bc}+\overrightarrow{cn}.\)
Cộng mỗi bên để có: \(\overrightarrow{mn}=\frac{1}{2}\left ( \overrightarrow{ad}+\overrightarrow{bc} \right ) )
hai)
\(\eqalign{ & \overrightarrow {mn} = \overrightarrow {ma} + \overrightarrow {ac} + \overrightarrow {cn} \cr & \overrightarrow {mn} = \overrightarrow {mb} + \overrightarrow {bd} + \overrightarrow {dn} \cr} \)
Cộng mỗi bên để có: \(\overrightarrow{mn}=\frac{1}{2}\left ( \overrightarrow{ac}+\overrightarrow{bd} \right ) . \)
Bài 5 Trang 92 SGK Hình Học 11
Cho tứ diện \(abcd\). Xác định hai dấu chấm \(e, f\) như thế này:
a) \(\overrightarrow{ae}=\overrightarrow{ab}+\overrightarrow{ac}+\overrightarrow{ad};\)
b) \(\overrightarrow{af}=\overrightarrow{ab}+\overrightarrow{ac}-\overrightarrow{ad}.\)
NGƯỜI CHIẾN THẮNG
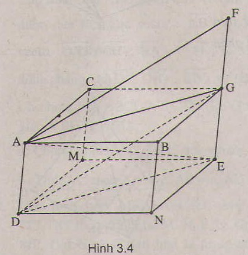
(h.3.4)
a) \(\overrightarrow{ab}+\overrightarrow{ac}=\overrightarrow{ag}\) trong đó \(g\) là đỉnh của hình bình hành\(abgc ).Ta có:
\(\overrightarrow{ag}+\overrightarrow{ad}=\overrightarrow{ae}\rightarrow\) \(e\) là đỉnh của hình bình hành\(adeg ).
b) Ta có \(\overrightarrow{ag}-\overrightarrow{ad}=\overrightarrow{af}\rightarrow\) \(f\) là đỉnh của hình bình hành (adgf\).
giaibaitap.me
Nguồn: https://dongnaiart.edu.vn
Danh mục: Tin tức
Lời kết: Trên đây là bài viết Giải bài 1, 2, 3, 4, 5 trang 91, 92 Sách giáo khoa Hình học 11. Hy vọng với bài viết này bạn có thể giúp ích cho bạn trong cuộc sống, hãy cùng đọc và theo dõi những bài viết hay của chúng tôi hàng ngày trên website: Dongnaiart.edu.vn
