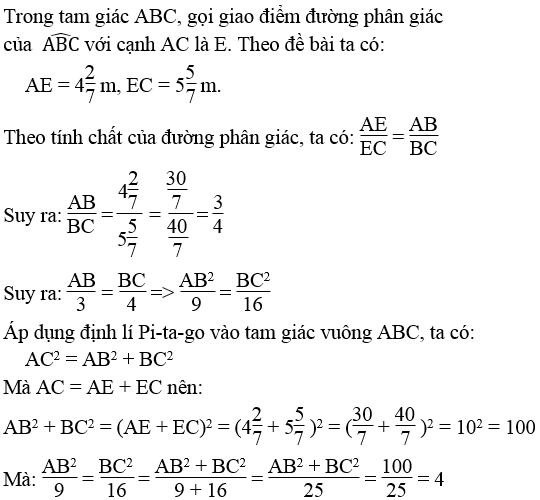Bạn đang xem: Giải sách bài tập Toán 9 Tập 1 trang 102, 103, 104, 105 (Đầy đủ) Tại DongnaiArt

Giải toán lớp 9 có đáp án: Bài 1: Hệ thức về cạnh và đường cao của tam giác vuông, Được tổ chức và xuất bản. Lời giải này kèm theo các phương pháp giải bài tập hay, được sắp xếp trong sách bài tập Toán 9, là tài liệu tham khảo hữu ích cho học sinh và giáo viên tham khảo, xử lý. Các mục đã trả lời chính xác, sẵn sàng để tiếp thu, dạy bài học mới một cách hiệu quả.

Bài 1: Một Số Mối Quan Hệ Giữa Cạnh Và Độ Cao Của Tam Giác Vuông

Bài tập 1 Trang 102 Sách bài tập Toán 9 Tập 1:

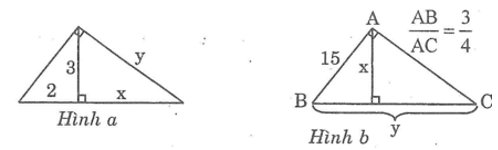
Tính x và y trong hình bên dưới:

Giải pháp thay thế:

Một. Hình 1:

Theo định lý Pitago, ta có:

Theo hệ thức giữa cạnh góc vuông và hình chiếu của nó, ta có:

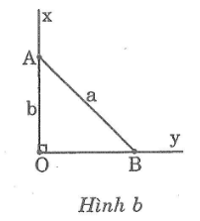
b. Hình b:

Theo quan hệ giữa cạnh góc vuông và phép chiếu ta có:

142 = y.16

x + y = 15 ⇒ x = 16 – y = 16 – 12,25 = 3,75.

Bài 2 Trang 102 Sách bài tập Toán 9 Tập 1:

Tính x và y trong hình bên dưới:

Giải pháp thay thế:

Một. Hình 1:

Theo quan hệ giữa cạnh góc vuông và phép chiếu ta có:

x2 = 2. (2 + 6) = 2,8 = 16 ⇒ x = 4

y2 = 6.(2 + 6) = 6,8 = 48 ⇒ y = √48 = 4√3

b. Hình b:

Theo hệ thức giữa chiều cao và hai hình chiếu hình chữ nhật, ta có:

x2 = 2,8 = 16 x = 4.

Bài tập 3 Trang 103 Sách bài tập Toán 9 Tập 1:

Tính x và y trong hình bên dưới:

Giải pháp thay thế:

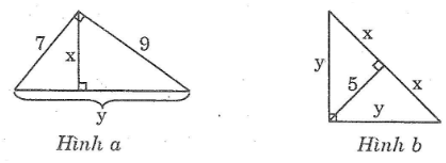
a.Hình ảnh a:

Theo định lý Pitago, ta có:

y2 = 72 + 92 y =

Theo hệ thức giữa chiều cao và cạnh của tam giác vuông, ta có:

x.y = 7,9 ⇒ x =

Hình b:

Theo quan hệ giữa độ cao và hình chiếu, ta có:

52 = x.x = x2 x = 5

Theo quan hệ giữa cạnh góc vuông và phép chiếu ta có:

y2 = x.(x + x) = 5.(5 + 5) = 50 ⇒ y = √50 = 5√2.

Bài 4 Trang 103 Sách Bài Tập Toán 9 Tập 1:

Tính x và y trong hình bên dưới:

Giải pháp thay thế:

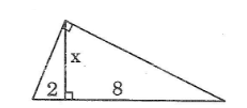
a.Hình ảnh a:

Theo quan hệ giữa độ cao và hình chiếu, ta có:

32 = 2.x ⇒ x = = 4.5

Theo quan hệ giữa cạnh góc vuông và phép chiếu ta có:

y2 = x.(x + 2) = 4,5.(4,5 + 2) = 29,25 ⇒ y = √29,25

b. Hình b:

Ta có: = 4,5 = 20

Theo định lý Pitago, ta có:

y2 = bc2 = ab2 + ac2 = 152 + 202 = 625

Suy ra: y = 625 = 25

Theo hệ thức giữa chiều cao và cạnh của tam giác vuông, ta có:

x.y = 15,20 x = = 12.

Bài 5 Trang 103 Sách bài tập Toán 9 Tập 1:

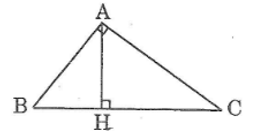
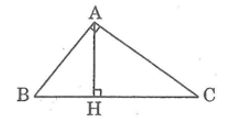
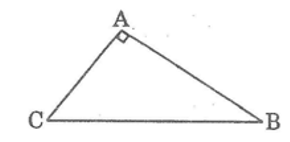
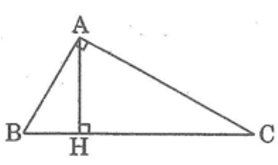
Cho tam giác abc, góc vuông a, chiều cao ah. Giải quyết từng trường hợp sau:

A. Cho ah = 16, bh = 25. Tính ab, ac, bc, ch

Cho ab = 12, bh = 6. Tính ah, ac, bc, ch

Giải pháp thay thế:

Một. Theo hệ thức giữa độ cao và hình chiếu ta có: ah2 = bh.ch

⇒ch =

bc = bh + ch = 25 + 10,24 = 35,24

Theo quan hệ giữa cạnh góc vuông và phép chiếu ta có:

ab2 = bc.bh ab =

≈ 29,68

ac2 = hc.bc

⇒ac = 18,99

b.Theo quan hệ giữa cạnh góc vuông và hình chiếu, ta có:

ab2 = bh.bc bc = = 24

ch = bc – bh = 24 – 6 = 18

Theo quan hệ giữa các cạnh của góc vuông và phép chiếu ta có:

ac2 = hc.bc ac = 20,78

Theo hệ thức giữa chiều cao và hình chiếu đứng ta có:

ah2 = hb.bc ah = .

Bài 6 Trang 103 Sách bài tập Toán 9 Tập 1:

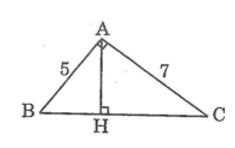
Đối với tam giác vuông có độ dài các cạnh lần lượt là 5 và 7, hãy vẽ chiều cao tương ứng với cạnh huyền. Tính chiều cao này và đường phân chia của nó trên cạnh huyền.

Giải pháp thay thế:

Giả sử tam giác abc có , ab = 5, ac = 7

Theo định lý Pitago, ta có:

bc2 = ab2 + ac2

Xem Thêm : Định nghĩa Tình yêu là gì? Quan niệm về Tình yêu chân chính

⇒ BC =

Theo hệ thức giữa chiều cao và cạnh của tam giác vuông, ta có:

ah.bc = ab.ac ah =

Theo hệ thức giữa cạnh góc vuông và hình chiếu của nó, ta có:

ab2 = bh.bc bh =

ch = bc – bh =

Bài 7 trang 103 sách bài tập toán 9 tập 1:

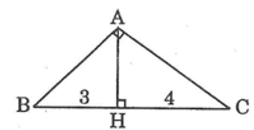
Chiều cao của tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 3 và 4. Tính các cạnh của tam giác này.

Giải pháp thay thế:

Giả sử tam giác abc có góc bac = 90o, ah ⊥ bc, bh = 3, ch = 4

Theo quan hệ giữa cạnh góc vuông và phép chiếu ta có:

ab2 = bh.bc = 3.(3 + 4) = 3,7 = 21 ⇒ ab = √21

ac2 = ch.bc = 4.(3 + 4) = 4,7 = 28 ⇒ ac = √28 = 2√7.

Bài 8 trang 103 sách bài tập toán 9 tập 1:

Cạnh huyền của một tam giác vuông lớn hơn một trong các góc vuông là 1 cm và tổng hai cạnh góc vuông lớn hơn cạnh huyền là 4 cm. Tính các cạnh của tam giác vuông này.

Giải pháp thay thế:

Giả sử góc (bac) của tam giác abc = 90o

Theo đề bài ta có: bc – ab = 1 (cm) (1)

ab + ac – bc = 4 (cm) (2)

Từ (1) và (2) suy ra: bc – ab + ab + ac – bc = 4 + 1 = 5 (cm)

Theo định lý Pitago, ta có: bc2 = ab2 + ac2 (3)

Suy ra từ (1): bc = ab + 1 (4)

Thay (4) vào (3) ta có:

(ab + 1)2 = ab2 + ac2

⇔ ab2 + 2ab + 1 = ab2 + 52

⇔ 2ab = 24ab = 12 (cm)

Thay ab = 12 (cm) vào (1) ta được: bc = 12 + 1 = 13 (cm).

bài 9 trang 104 sách bài tập toán 9 tập 1:

Một tam giác vuông có cạnh huyền bằng 5, chiều cao ứng với cạnh huyền bằng 2, hãy tính cạnh nhỏ nhất của tam giác vuông này.

Giải pháp thay thế:

Giả sử tam giác abc có góc (bac) = 90o, ah ⊥ bc, bc = 5, ah = 2 và bh <; ch

Ta có: bh + ch = 5 (1)

Theo hệ thức giữa chiều cao và cạnh huyền của tam giác, ta có:

bh.ch = ah2 = 22 = 4 (2)

Suy ra từ (1) và (2): bh = 1 và ch = 4

Theo quan hệ giữa cạnh góc vuông và phép chiếu ta có:

ab2 = bh.bc = 1,5 = 5

Suy ra: ab = 5.

Bài 10 trang 104 sách bài tập toán 9 tập 1:

Một tam giác vuông. Tỉ lệ độ dài các cạnh góc vuông là 3:4 và cạnh huyền là 125 cm. Tính độ dài của chân và hình chiếu của chân lên cạnh huyền.

Giải pháp thay thế:

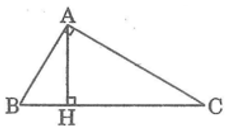
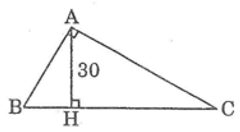
Bài 11 Trang 104 Sách bài tập Toán 9 Tập 1:

Tam giác abc vuông góc với a. Biết ab/ac=5/6, chiều cao ah=30cm. Tính hb, hc.

Giải pháp thay thế:

Bài 12 trang 104 sách bài tập toán 9 tập 1:

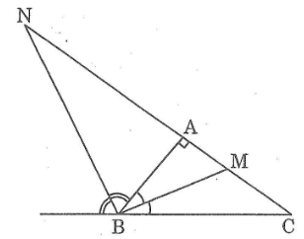
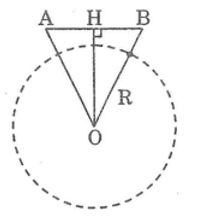
Nếu khoảng cách theo đường thẳng là 2200 km thì hai vệ tinh bay ở vị trí a và b ở cùng khoảng cách 230 km có thể nhìn thấy nhau không? Biết rằng bán kính r của trái đất là gần 6370 km và nếu ồ > thì hai vệ tinh sẽ nhìn thấy nhau

Giải pháp thay thế:

Vì hai vệ tinh cách mặt đất 230 km nên tam giác aob cân tại o.

Ta có: oa = r + 230

= 6370 + 230 = 6600 (km)

Trong tam giác aob ta có: ồ ab

Suy ra: ha = hb = ab/2 = 2200/2 = 1100 (km)

Áp dụng định lý Pitago cho tam giác vuông aho, ta có:

oa2 = ah2 + oh2

Suy ra: oh2 = oa2 – ah2

Suy luận:

oh = 6508 (km)

Vì oh> r để hai vệ tinh có thể nhìn thấy nhau.

Bài 13 Trang 104 Sách bài tập Toán 9 Tập 1:

Cho hai đoạn thẳng có độ dài a và b. Dựng các đoạn thẳng có độ dài bằng nhau:

Giải pháp thay thế:

Một. *Cách dựng (hình a):

– Tạo góc xoay vuông góc.

– Trên tia ox dựng đoạn oa = a

– Trên tia oy, dựng ob = b.

– nối ab ta có đoạn ab = cần dựng

*Chứng nhận:

Áp dụng định lý Pitago cho tam giác vuông aob, ta có:

ab2 = oa2 + ob2 = a2 + b2

Suy ra: ab =

b. *Cách dựng (Hình b):

– Tạo góc xoay vuông góc

– Trên tia ox dựng đoạn oa = b.

– Đường tròn tâm a bán kính a cắt oy tại b.

Chúng ta sẽ xây dựng ob = (a > b).

*Chứng nhận:

Áp dụng định lý Pitago cho tam giác vuông aob, ta có:

ab2 = oa2 + ob2 ⇒ ob2 = ab2 – oa2 = a2 – b2

Suy ra: ob =

Xem Thêm : xóa bảng trong excel

bài 14 trang 104 sách bài tập toán 9 tập 1:

Cho hai đoạn thẳng có độ dài a và b. Cách tạo đoạn thẳng √(ab)?

Giải pháp thay thế:

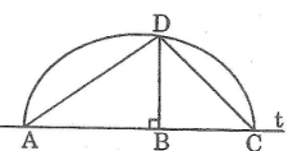
*Cách xây dựng:

– Dựng một dòng t.

– Dựng hai đoạn thẳng liên tiếp ab = a, bc = b trên đường thẳng t.

– Dựng nửa đường tròn tâm o, đường kính ac.

– Từ b kẻ đường vuông góc với ac cắt nửa đường tròn tâm o tại d

Chúng tôi muốn xây dựng một đoạn bd = √(ab​​).

*Chứng nhận:

Kết nối da với DC. Ta có acd vuông tại d và db ac.

Theo quan hệ giữa độ cao và hình chiếu, ta có:

bd2 = ab.bc = a.b

Suy ra: bd = (ab).

Bài 15 trang 104 sách bài tập toán 9 tập 1:

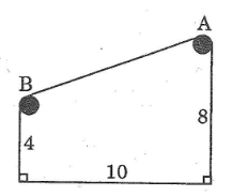
Giữa hai khu nhà của nhà máy (nhà kho và nhà xưởng) được xây dựng một băng tải ab để vận chuyển nguyên vật liệu. Khoảng cách giữa hai tòa nhà là 10m, hai vòng quay của băng chuyền được đặt ở độ cao 8m và 4m so với mặt đất. Tìm độ dài ab của băng chuyền.

Giải pháp thay thế:

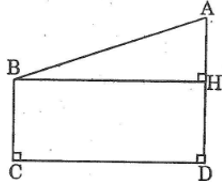
Kẻ đường thẳng bh ⊥ ad ta được tứ giác bcdh là hình chữ nhật.

Ta có: bc = dh và bh = cd (tính chất hình chữ nhật)

Suy ra: dh = 4(cm)

à = 8 – 4 = 4 (cm)

bh = 10 (cm)

Áp dụng định lý Pitago cho tam giác vuông abh, ta có:

ab2 = bh2 + ah2

Suy ra: ab = 10,8 (m)

Do đó, băng tải dài khoảng 10,8 m.

Bài 16 trang 104 sách bài tập toán 9 tập 1:

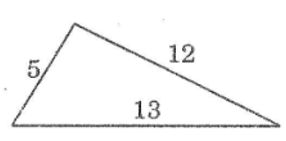
Cho tam giác có độ dài cạnh là 5, 12, 13, tìm góc đối diện với cạnh có độ dài 13 của tam giác.

Giải pháp thay thế:

Ta có: 52 + 122 = 25 + 144 = 169 = 132

Vì một tam giác có ba cạnh và độ dài các cạnh thỏa mãn định lý Pitago (bình phương một cạnh bằng tổng bình phương hai cạnh kia) nên tam giác đó là tam giác vuông.

Vậy góc đối diện với cạnh 13 (cạnh dài nhất) là góc vuông.

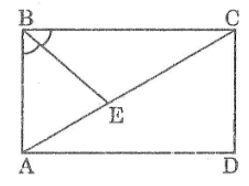
Bài 17 Trang 104 Sách bài tập Toán 9 Tập 1:

Cho hình chữ nhật abcd. Tia phân giác của góc b chia đường chéo ac thành hai đoạn m. Tính các kích thước của hình chữ nhật.

Giải pháp thay thế:

Suy ra: ab2 = 9,4 = 36 ⇒ ab = √36 = 6 (m)

bc2 = 16,4 = 64 bc = √64 = 8 (m)

Vậy: ab = cd = 6m

bc = ad = 8m.

Bài 18 trang 105 sách bài tập toán 9 tập 1:

Tam giác abc vuông góc với a. Vẽ một đường cao. Chu vi tam giác abh là 30 cm, chu vi tam giác ach là 40 cm. Tìm chu vi tam giác abc.

Giải pháp thay thế:

Gọi a, b, c lần lượt là chu vi các tam giác abc, abh, ach.

Ta có: b = 30cm, c = 40cm

Xét hai tam giác vuông ahb và cha, ta có:

Bài 19 trang 105 sách bài tập toán 9 tập 1:

Cho tam giác vuông abc có cạnh ab = 6cm và ac = 8cm. Các đường phân giác trong và ngoài của góc b lần lượt cắt đường thẳng ac tại m và n. Tính các đoạn thẳng am và an.

Giải pháp thay thế:

Vì bm là tia phân giác của góc b nên ta có:

Vì bn là tia phân giác của góc ngoài b nên ta có: bm ⊥ bn

Suy ra tam giác bmn tại b

Theo hệ thức giữa chiều cao và hai hình chiếu hình chữ nhật, ta có: ab2 = am.an

Suy ra: an = = 12 (cm).

Bài 20 trang 105 sách bài tập toán 9 tập 1:

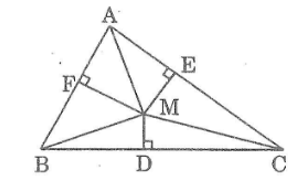
Tam giác vuông abc. Từ một điểm m bất kỳ trong tam giác, vẽ md, me, mf lần lượt vuông góc với các cạnh bc, ac, ab. Chứng minh: bd2 + ce2 + af2 = dc2 + ea2 + fb2

Giải pháp thay thế:

Áp dụng định lý Pitago cho tam giác vuông bdm, ta có:

bm2 = bd2 + dm2 => bd2 = bm2 – dm2 (1)

Áp dụng định lý Pitago cho tam giác vuông cem, ta có:

cm2 = ce2 + en2 => ce2 = cm2 – em2 (2)

Áp dụng định lý Pitago cho tam giác vuông afm, ta có:

am2 = af2 + fm2 => af2 = am2 – fm2 (3)

Cộng từng vế của (1), (2) và (3), ta được:

bd2 + ce2 + af2 = bm2 – dm2 + cm2 – em2 + am2 – fm2 (4)

Áp dụng định lý Pitago cho tam giác vuông bfm, ta có:

bm2 = bf2 + fm2 (5)

Áp dụng định lý Pitago cho tam giác vuông cdm, ta có:

cm2 = cd2 + dm2 (6)

Áp dụng định lý Pitago cho tam giác vuông aem, ta có:

am2 = ae2 + em2 (7)

Thay (5), (6) và (7) vào (4) ta có:

bd2 + ce2 + af2

= bf2 + fm2 – dm2 + cd2 + dm2 – em2 + ae2 + em2 – fm2

= dc2 + ea2 + fb2

Vậy bd2 + ce2 + af2 = dc2 + ea2 + fb2.

Ngoài ra, các em học sinh và thầy cô có thể liên tục cập nhật thêm nhiều tài liệu bổ ích ở tất cả các môn học trên website của chúng tôi.

►►Nhấn nút Tải xuống bên dưới để tải ngay Đáp án trang 102, 103, 104, 105 Sách bài tập Toán 1: Tr. Bài 1: Một số hệ thức giữa các cạnh và chiều cao của tam giác vuông