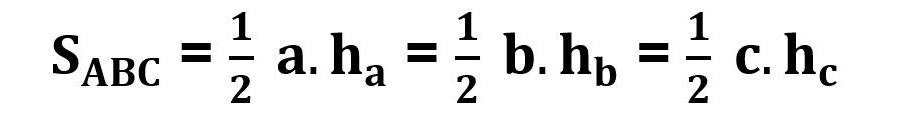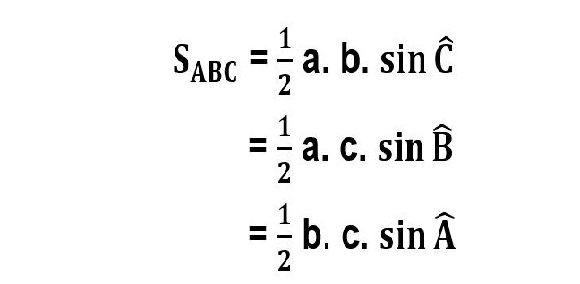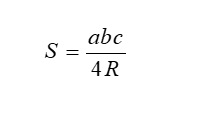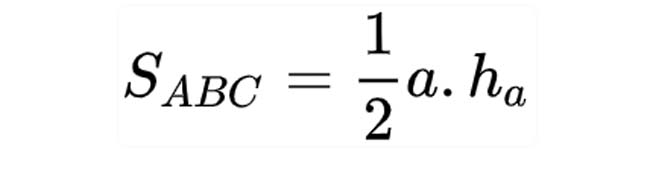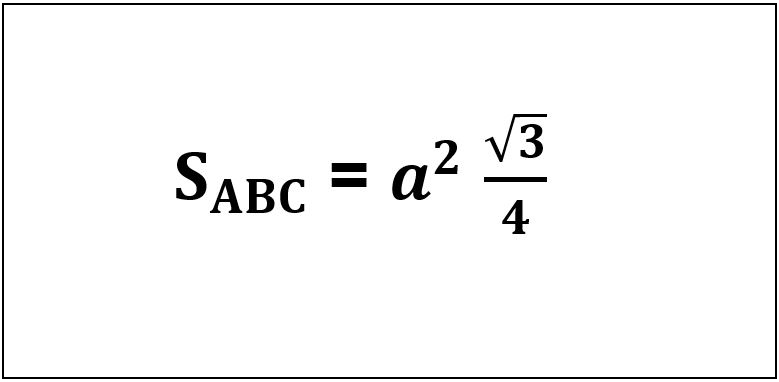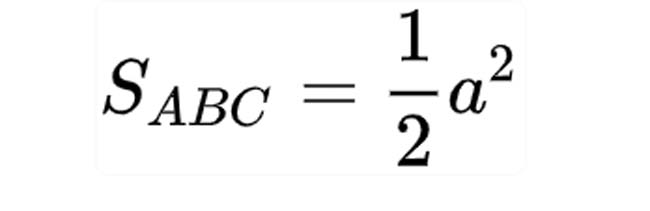Cùng xem Công thức tính diện tích tam giác vuông, cân, đều, thường – Legoland trên youtube.
Việc chọn đúng công thức tính diện tích tam giác vuông, vuông cân, tam giác vuông cân, tam giác đều không chỉ giúp chúng ta giải nhanh một bài toán mà còn giúp các em có một đáp án chuẩn khác. Hầu hết chúng ta đều đã học công thức tính diện tích tam giác từ thời phổ thông, tuy nhiên một số người đã quên mất sau một thời gian dài không sử dụng, vì vậy hôm nay Legoland xin tổng hợp lại công thức tính diện tích tam giác. tam giác vuông, tam giác cân. Dành cho tất cả mọi người.
Có bao nhiêu loại hình tam giác?
Đối với hình tam giác, chúng ta sẽ có các loại hình tam giác sau:
- Tam giác vuông
- Tam giác cân
- Tam giác vuông cân
- Tam giác đều
- Tam giác đều
- 5 ví dụ về công thức tính diện tích và chu vi hình bình hành
- Tính thể tích và diện tích hình chóp tứ giác đều
- Công thức tính diện tích hình trụ và hình nón tiêu chuẩn
- Công thức tính thể tích của hình nón và hình trụ tiêu chuẩn
- p: Chu vi tam giác.
- a,b,c: là ba cạnh của tam giác đều
- a, b, c: lần lượt là độ dài các cạnh của tam giác.
- ha, hb, hc: lần lượt là các đường cao nối với nhau qua các đỉnh a, b, c.
- a, b, c: lần lượt là độ dài các cạnh của tam giác.
- p: Nửa chu vi tam giác, bằng ½ tổng các cạnh của tam giác.
- a, b, c: lần lượt là độ dài các cạnh của tam giác.
- r: Bán kính đường tròn ngoại tiếp.
- Trong tam giác cân, 2 cạnh bên bằng nhau, 2 góc ở đáy bằng nhau.
- Tam giác vuông cân là tam giác vuông có 2 cạnh hoặc 2 góc ở đáy bằng nhau.
- Hẻm độ cao từ trên xuống dưới trong tam giác cân cũng chính là đường trung tuyến và phân giác của tam giác.
- p: Chu vi tam giác.
- a, b, c: lần lượt là 3 cạnh của tam giác.
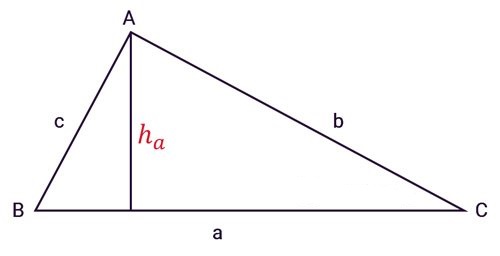
- a : độ dài cạnh của tam giác
- ha : chiều cao của đỉnh vuông góc với cạnh đối diện
- Mỗi góc của tam giác đều bằng 60 độ
- Một tam giác đều nếu nó có ba góc bằng nhau
- Một tam giác cân là tam giác đều nếu các góc trong của nó bằng 60 độ
- Tam giác có ba cạnh bằng nhau là tam giác đều
- Tam giác có ba góc bằng nhau là tam giác đều
- Tam giác cân có góc trong bằng 60 độ là tam giác đều
- Tam giác có các góc trong bằng 60 độ là tam giác đều
- p: Chu vi tam giác đều.
- a: Độ dài cạnh của tam giác.
- ah : chiều cao của tam giác tính từ đỉnh a đến bc
- bc : là độ dài cạnh bc
- a: Độ dài cạnh của tam giác đều.
- Tam giác có một góc vuông là tam giác vuông
- Tam giác có hai góc nhọn bù nhau là tam giác vuông
- Tam giác có bình phương một cạnh bằng tổng bình phương hai cạnh còn lại là tam giác vuông
- Cạnh tương ứng với đường trung tuyến của tam giác bằng một nửa cạnh là tam giác vuông
- Tam giác nội tiếp có các cạnh là đường kính của hình tròn là tam giác vuông
- a,b,c là độ dài các cạnh của tam giác
- a , b : là độ dài hai cạnh góc vuông
Xem chi tiết bài giảng về diện tích tam giác
Điều kiện tính diện tích tam giác:
Trên thực tế ta không chỉ tính được diện tích tam giác này mà còn phụ thuộc vào rất nhiều yếu tố khác. Nhưng để tính diện tích, chúng ta cần một số tham số tối thiểu, chẳng hạn như số đo góc, độ dài các cạnh hay chu vi…
Tham khảo phương pháp tính toán của diện tích hình dạng khác:
Các công thức tính diện tích tam giác đều, cân, tam giác đều, tam giác đều
Công thức tính diện tích tam giác chung
Định nghĩa
Tam giác thường là tam giác có độ dài các cạnh khác nhau và các góc trong khác nhau.
Cách tính chu vi tam giác thường
Chu vi tam giác đều bằng tổng độ dài 3 cạnh. Do đó, chúng ta có thể áp dụng công thức sau:
p = a + b + c
Ở đâu:
Ví dụ: Cho tam giác có 3 cạnh là 3 cạnh: ab = 5cm, bc = 6cm, ac = 4cm. Tính chu vi hình tam giác?
Áp dụng công thức trên ta tính được chu vi tam giác: p = 5 + 6 + 4 = 15cm
=>Chu vi hình tam giác là: 15cm
Công thức tính diện tích tam giác đã biết chiều cao
Diện tích tam giác bằng ½ chiều cao của đỉnh nhân với độ dài cạnh đối diện với đỉnh.
Ở đâu:
Ví dụ: Cho tam giác abc có các cạnh là: ab = 2cm, chiều cao của đỉnh a vuông góc với cạnh bc là 6cm. Tính diện tích tam giác abc?
Áp dụng công thức trên ta sẽ tính được diện tích tam giác như sau:
Diện tích tam giác abc = 1/2 * (2* 6) = 6cm2
Công thức tính diện tích tam giác thường có một góc cho trước
Công thức diện tích tam giác abc là tích của ½ hai cạnh kề và sin của góc giữa hai cạnh đó của tam giác.
Ví dụ: Tính diện tích tam giác abc có cạnh ab = 3cm, cạnh bc = 4cm, góc abc = 30 độ
Áp dụng công thức ta tính được điện tích của tam giác abc = 1/2*(3 * 4 * sin 30 độ)
Dùng công thức Heron để tính diện tích tam giác
Ở đâu:
Công thức tính diện tích tam giác khi biết bán kính đường tròn ngoại tiếp tam giác
Khi biết độ dài ba cạnh và bán kính r của đường tròn ngoại tiếp tam giác, ta áp dụng công thức sau:
Vị trí:
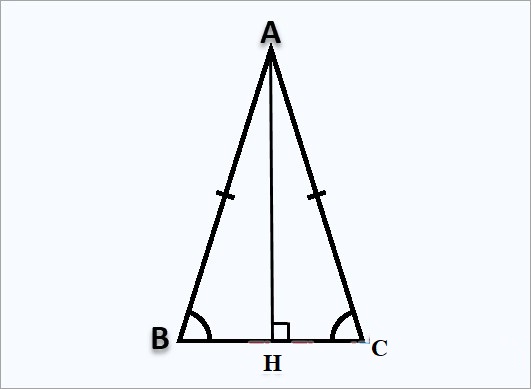
Công thức tính diện tích tam giác cân
Trước khi vào công thức tính diện tích tam giác cân, chúng ta cần hiểu bản chất của tam giác cân là gì. Chi tiết như sau:
Định nghĩa
Xem Thêm : Fet là gì? Mosfet là gì? Bài viết hay nhất, chi tiết nhất về Mosfet
Tam giác cân là tam giác có hai cạnh bằng nhau và góc ở đáy bằng nhau.
Tính năng
Tam giác cân là tam giác bên trong có các tính chất sau:
Công thức tính chu vi tam giác cân
Một tam giác cân có tích bằng một tam giác thường nên chu vi của nó được tính theo cách tương tự:
p = a + b + c
Ở đâu:
Công thức tính diện tích tam giác cân
Tính diện tích tam giác cân cũng giống như công thức tính diện tích tam giác đều, ngoài ra còn tính theo chiều cao.
Ở đâu:
Ví dụ: Tam giác acb cân tại c, gọi h là trung điểm của cạnh ab, cạnh ac = 8 cm, ch = 13 cm. Tính diện tích tam giác acb.
Giải pháp thay thế:
Bài toán có chiều cao ch = 13 cm, cạnh đáy ac = 8 cm.
Áp dụng công thức tính diện tích ta được: s = 1⁄2 a.h = 1⁄2 x 13 x 8 = 52 cm2
=>Khi đó diện tích tam giác cân acb là: 52cm2
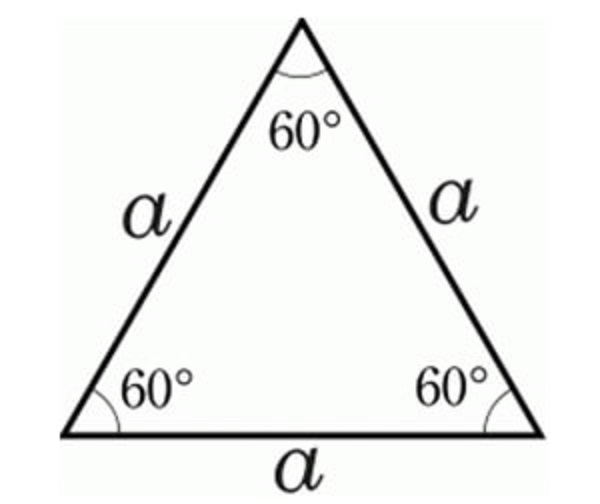
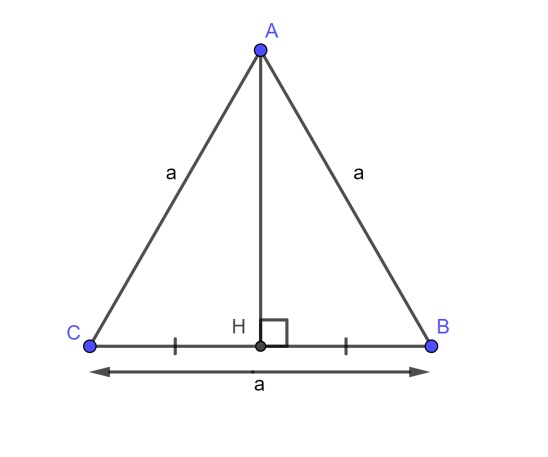
Công thức tính diện tích tam giác đều
Theo mình công thức tính diện tích tam giác đều thường đơn giản và dễ dàng hơn so với cách tính diện tích các tam giác khác.
Định nghĩa
Tam giác đều là tam giác có 3 cạnh bằng nhau, 3 chiều cao, 3 đường trung tuyến và 3 đường phân giác bằng nhau hoặc bằng nhau với 3 góc trong bằng 60°
Tính năng
Công thức tính chu vi
Vì tam giác đều có 3 cạnh bằng nhau nên chu vi tam giác bằng 3 lần 3 cạnh bất kỳ
p = 3 * a
Ở đâu:
Cách tính diện tích tam giác đều
Vì tam giác abc là tam giác đều nên đường cao kẻ từ đỉnh a trùng với đường trung trực đỉnh a của tam giác abc
Công thức tính diện tích tam giác abc là
Ở đâu:
Ngoài ra, bạn áp dụng công thức Heron để tính:
Ở đâu:
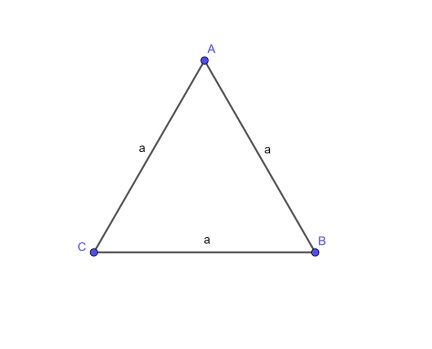
Ví dụ: Bạn có một tam giác đều abc với các cạnh dài 8 cm và bạn biết rằng các góc trong của tam giác này là 60 độ. Diện tích tam giác đều abc là bao nhiêu?
Trả lời: Vì mỗi cạnh ab = ac = bc = 8cm nên ta có độ dài cạnh a = 8cm.
Áp dụng công thức Herron ta tính được diện tích tam giác đều:
Xem Thêm : Chill là gì? Chill phết là gì? Đi chill là gì?
s = a2 x (√3)/4 = s = 64 x (√3)/4 = 64 x (√3)/4 = 64 x (1.732/4) = 27.712 cm2
Vậy diện tích tam giác đều abc = 27,712 cm2
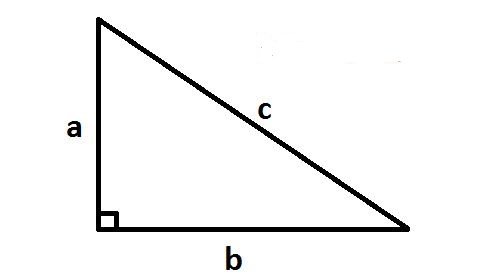
Công thức tính diện tích tam giác vuông
Để tính diện tích tam giác vuông trước tiên chúng ta cần hiểu tam giác vuông là gì và cách nhận biết trước.
Định nghĩa
Tam giác vuông là tam giác có một góc vuông (góc 900)
Cách xác định tam giác vuông
Công thức tính chu vi
p = a + b + c
Ở đâu:
Công thức tính diện tích tam giác vuông
Để tính điện tích của một tam giác vuông, ta có thể áp dụng công thức:
Ở đâu:
Ví dụ: Cho tam giác vuông abc, góc b vuông góc. Tính diện tích tam giác vuông biết hai góc vuông là ab = 4cm và bc = 7cm
Trả lời:
Áp dụng công thức trên vào cách tính diện tích tam giác vuông, ta tính được như sau:
s = (4 x 7) : 2 = 14 (cm2)
=>Khi đó diện tích tam giác vuông abc là: 14cm2
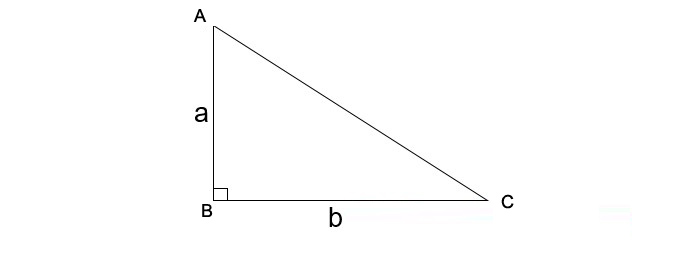
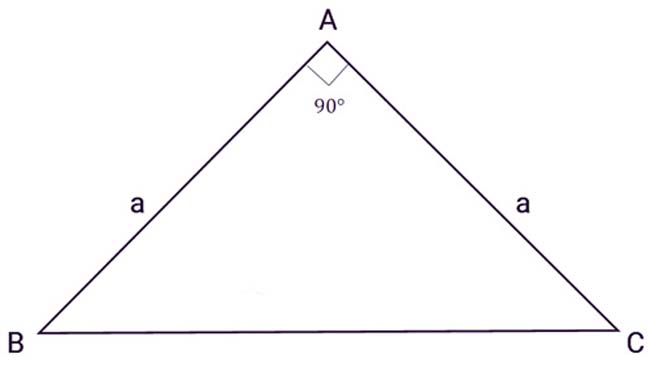
Công thức tính diện tích tam giác vuông cân
Định nghĩa
Tam giác vuông cân là tam giác có hai cạnh bằng nhau
Thuộc tính
Về tính chất của tam giác vuông cân, chúng ta sẽ có 2 tính chất khác nhau:
Tính chất 1: Một tam giác vuông cân có hai góc ở đáy bằng nhau và bằng 45 độ
Tính chất 2: Đường cao, đường trung trực và đường phân giác của các đỉnh góc vuông của một tam giác cân trùng nhau và bằng một nửa cạnh huyền.
Ta có: Xét tam giác abc vuông góc với a. Gọi d là trung điểm của bc. Ta có ad là chiều cao, tia phân giác và trung tuyến của bc. ad = bd = dc = 1/2bc
Công thức tính diện tích tam giác vuông cân
Công thức chuẩn để tính diện tích tam giác vuông cân như sau:
Ví dụ: Cho tam giác abc vuông góc với a, ab = ac = 10 cm. Tính diện tích tam giác abc theo công thức tính diện tích tam giác trên.
Trả lời:
Cạnh ab=ac=a=10cm
Xét tam giác abc vuông góc với a, ta có:
s = (a2) : 2 = 100 : 2 = 50 cm2
Vậy ta có diện tích tam giác vuông cân abc sẽ là: 50 cm2
Tóm tắt:
Kết hợp với các công thức tính diện tích tam giác vuông, tam giác đều, tam giác cân và tam giác vuông cân trên đây, hi vọng các bạn có thể tích lũy thêm kinh nghiệm và nâng cao kiến thức sắp xếp, tinh chỉnh legoland.
Nguồn: https://dongnaiart.edu.vn
Danh mục: Tin tức
Lời kết: Trên đây là bài viết Công thức tính diện tích tam giác vuông, cân, đều, thường – Legoland. Hy vọng với bài viết này bạn có thể giúp ích cho bạn trong cuộc sống, hãy cùng đọc và theo dõi những bài viết hay của chúng tôi hàng ngày trên website: Dongnaiart.edu.vn