Cùng xem Vô hạn là gì? – Toán học lý thú trên youtube.

Hiểu biết của chúng ta về thế nào là một câu hỏi vô hạn là rất mơ hồ. Vô cực là đặc tính của một thứ không bao giờ kết thúc: một vũ trụ vô tận, hay một danh sách không bao giờ kết thúc, như danh sách các số tự nhiên 1, 2, 3, 4,… dù bạn có đếm bao lâu đi nữa, nhưng bạn không bao giờ hết. Sẽ tìm ra con số cuối cùng, bạn thậm chí không thể kết thúc vũ trụ vô tận, ngay cả khi bạn du hành trên con tàu vũ trụ nhanh nhất. Các vô hạn trên được gọi là vô hạn tiềm năng bởi nhà toán học Hy Lạp cổ đại Aristotle. Vô cực tồn tại, nhưng bạn không bao giờ gặp nó trực tiếp. Bạn không bao giờ đi đến cuối một danh sách khổng lồ hoặc không bao giờ kết thúc.
Aristotle cũng phản ánh về một loại vô cực khác, được gọi là vô cực thực tế, là thứ bạn có thể đo lường, chẳng hạn như biểu thị nhiệt độ của một vật thể tại một địa điểm và thời gian cụ thể. Không ai từng nhìn thấy một thực tại vô tận, và thực sự Aristotle tin rằng không có thực tại vô hạn trong thế giới vật chất. Cho đến ngày nay, các nhà vật lý vẫn không biết ông đúng hay sai.
I. Hãy cẩn thận khi đếm.
Vậy thì chúng ta hãy hiểu tiềm năng vô tận, đặc tính của những thứ vô hạn. Chúng ta đã học xong các số tự nhiên, nhưng bây giờ hãy tưởng tượng một hàng dài vô tận, một hàng bắt đầu trước mặt bạn và kéo dài mãi mãi. Vô cực này có giống với vô cực được biểu diễn bằng các số tự nhiên không?
Theo trực giác, bạn có thể nghĩ rằng hai số này khác nhau, nghĩ rằng các số tự nhiên là riêng biệt và tồn tại riêng biệt, trong khi các đường kẻ tạo thành một trường liên tục. Bạn có thể đặt các số tự nhiên dọc theo con đường của mình với khoảng cách 1 mét. Điều này tạo ấn tượng rằng vô cực của dòng lớn hơn vô cực của các số tự nhiên, bởi vì các đoạn thẳng có thể lấp đầy khoảng trống giữa các số.
Các nhà toán học đồng ý với trực giác của họ. Họ phân biệt giữa các khái niệm vô hạn đếm được và vô hạn không đếm được. Các số tự nhiên tạo thành một phạm vi đếm được vô hạn, khiến bạn có cảm giác như nếu bạn có thời gian vô hạn, bạn có thể đếm hết chúng. Một nhóm lớn vô hạn cũng được coi là vô hạn đếm được. Đó là bởi vì trong thời gian vô hạn, bạn có thể tạo một danh sách tất cả các tên, mỗi tên có một vị trí riêng trong danh sách, và sau đó bạn cũng có thể đếm chúng, giống như bạn có thể đếm các số tự nhiên. Nói chung, một tập hợp vô hạn các đối tượng sẽ tạo thành vô số vô số, nếu bạn có thể liệt kê từng đối tượng một, mỗi đối tượng có một vị trí trong danh sách, cho mỗi vị trí trong danh sách. Danh sách sẽ có một đối tượng.
Còn những hàng dài vô tận thì sao? Các đường cũng bao gồm vô số đối tượng. Trong trường hợp này, các đối tượng là các điểm trên đường thẳng. Nếu bạn tưởng tượng đường thẳng là thước đo có chiều dài vô hạn, thì mỗi điểm có một số. Điểm đầu của vạch là số 0, điểm nửa thước là số 0,5 v.v… (tập hợp các số thu được từ thước gọi là số thực dương). Bạn có thể tạo một danh sách các số để chỉ ra rằng những số này cũng mang lại các phạm vi vô hạn có thể đếm được không?
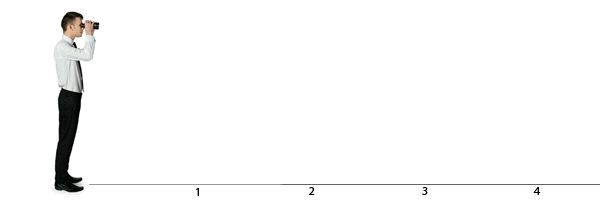
Xem Thêm : mau bien ban hop phu huynh
Một giải pháp là chúng tôi có thể sắp xếp các số theo kích thước, nhưng điều đó sẽ khiến bạn gặp rắc rối rất nhanh. Rõ ràng là số đầu tiên phải bằng 0, bạn nghĩ gì về số thứ hai? . Bạn có thể thử 0,1, nhưng 0,01 nhỏ hơn, vì vậy 0,01 phải đến trước 0,1. Nhưng còn 0,001 thì sao? Đối với mỗi số, bạn có thể chỉ ra rằng số ở vị trí thứ hai trong danh sách nhỏ hơn số đó (bạn chỉ cần chèn số 0 sau dấu thập phân). Vì vậy, việc tạo danh sách các số được sắp xếp theo kích thước là vô ích.
Có lẽ có một cách khác để liệt kê chúng? Câu trả lời là không. Có một lập luận đơn giản rằng bất kỳ danh sách các số thực dương nào chắc chắn sẽ bỏ sót ít nhất một số thực dương khác. Bạn không bao giờ có thể lập một danh sách đầy đủ. Điều này chứng tỏ rằng vô cực của một đường thẳng dài vô hạn (hoặc các số thực dương tương đương,…) là vô cực không đếm được.
Hai. Vô cực nào?
Bạn nghĩ gì về ý kiến cho rằng vô cực của một số đường thẳng vô hạn “lớn hơn” so với vô cực của các số tự nhiên? Nếu bạn cảm thấy mệt mỏi với việc đếm, có một cách để so sánh kích thước của một số tập hợp hữu hạn và đó là kiểm tra xem các phần tử của mỗi tập hợp có khớp nhau không. Hãy nghĩ về số ghế và số người, nếu mỗi người có một chiếc ghế và không còn ghế nào, thì bạn biết rằng số ghế bằng số người. Nếu có ghế trống, bạn biết rằng có nhiều ghế hơn số người, và nếu bạn đang đứng, bạn biết rằng có nhiều người hơn số ghế.
Bạn có thể thêm ý tưởng này vào bộ sưu tập đối tượng không giới hạn. Nếu bạn có thể ghép chính xác các đối tượng trong tập hợp a với các đối tượng trong tập hợp b và mỗi đối tượng trong tập hợp a tương ứng với chính xác một đối tượng trong tập hợp b và ngược lại, thì ta nói hai tập hợp có cùng kích thước, trong toán học được gọi là số phần tử trong cùng một bộ. Chúng tôi thấy điều này ở vô số người kể trên. Bằng cách liệt kê lần lượt, ta đã thực sự ghép đúng với các số tự nhiên, mỗi người có đúng một số tự nhiên (vị trí của mình trong danh sách) và mỗi số tự nhiên tất nhiên có đúng một người (chiếm vị trí này trong danh sách đã cho). bằng vị trí của số tự nhiên s). Đó là lý do tại sao chúng ta nói rằng các đám đông và các số tự nhiên đại diện cho cùng một loại vô hạn—vô số đếm được.
Trở về một điểm trên một đường dài vô tận. Bất kể, dòng cho thấy rằng đối với bất kỳ nỗ lực nào để liệt kê các điểm (được tìm thấy chính xác với các số tự nhiên), chúng tôi vẫn sẽ bỏ lỡ ít nhất một điểm. Đây là lý do tại sao chúng ta nói rằng số phần tử trong tập hợp các đường thẳng (vô hạn và không đếm được) lớn hơn số phần tử trong tập hợp các số tự nhiên (vô hạn đếm được).
Ba. Rào cản đếm được
Theo trực giác, số vô hạn không đếm được có vẻ rắc rối (ngay cả trong toán học) và đòi hỏi sự khéo léo và phức tạp hơn so với số vô hạn đếm được. Nhưng điều đó không có nghĩa là vô số đếm được là dễ hiểu. Ví dụ, hãy xem xét rằng có vô số các số chẵn 2, 4, 6, 8, …, nhưng làm thế nào để số phần tử trong một tập hợp (kích thước) vô hạn như vậy so với tất cả các số tự nhiên? bằng một nửa?
Câu trả lời là không. Chúng ta giả sử rằng nếu mọi đối tượng trong một có thể khớp chính xác với mọi đối tượng trong đối tượng kia, thì hai tập hợp vô hạn được cho là có cùng số phần tử trong một tập hợp, thì thật dễ dàng khớp chính xác mọi số chẵn với mọi số tự nhiên .
$$1\ đến 2$$
Xem Thêm : Suy nghĩ về cái chết của lão hạc 2023 – sgkphattriennangluc.vn
$$2\ đến 4$$
$$3\đến 6$$
$$4\ đến 8$$
Vậy tập hợp các số chẵn có cùng số phần tử với tập hợp các số tự nhiên. Nếu điều đó nghe có vẻ kỳ lạ, kết quả tiếp theo có thể còn kỳ lạ hơn. Chúng ta có thể chỉ ra rằng tất cả các số hữu tỷ (nghĩa là tất cả các phân số như 1/2 hoặc 5/6) cũng là đếm được, có nghĩa là chúng cũng có thể được kết hợp chính xác với các số tự nhiên. Do đó, cho dù phân số xuất hiện nhiều hơn số tự nhiên (có vô số phân số nằm giữa hai số tự nhiên liên tiếp bất kỳ) thì số phần tử của hai tập hợp số là như nhau. tụ họp.
Vào thế kỷ 17, Galileo Galileo lỗi lạc đã khám phá ra những điều kỳ diệu về sự vô tận và những suy nghĩ kỳ lạ về sự vô tận. Điều này khiến anh ấy không còn suy nghĩ về vô hạn và tuyên bố rằng “chúng ta không thể nói rằng một số vô hạn lớn hơn hoặc nhỏ hơn hoặc bằng một số vô hạn khác”. Hơn 200 năm sau, nhà toán học George Cantor đã tinh chỉnh lại những ý tưởng này. Anh ta không bị đe dọa bởi sự kỳ lạ của vô cực, và đi xa hơn, anh ta tìm thấy những tòa tháp vô cực hoàn chỉnh, cái này lớn hơn cái kia. Vô số số tự nhiên và vô số đường thẳng thỏa mãn các tính chất của kim tự tháp này.
George Cantor
Tất cả những điều này liên quan đến tiềm năng vô hạn, một danh sách rộng lớn và không bao giờ kết thúc. Điều gì xảy ra với thực sự vô hạn? Có thực sự có bất kỳ loại vô hạn trong thế giới vật chất?
Nguồn: https://plus.maths.o…t/what-infinity
Bài viết được dịch bởi các thành viên tạp chí exp.
Bài viết này đã được chỉnh sửa bởi hoangtrong2305: 18-01-2016 – 23:15
Nguồn: https://dongnaiart.edu.vn
Danh mục: Tin tức
Lời kết: Trên đây là bài viết Vô hạn là gì? – Toán học lý thú. Hy vọng với bài viết này bạn có thể giúp ích cho bạn trong cuộc sống, hãy cùng đọc và theo dõi những bài viết hay của chúng tôi hàng ngày trên website: Dongnaiart.edu.vn




