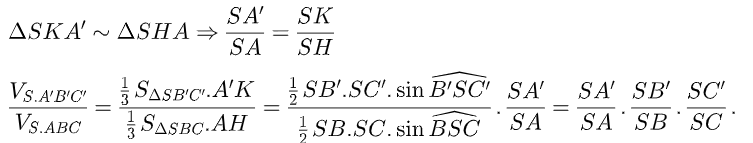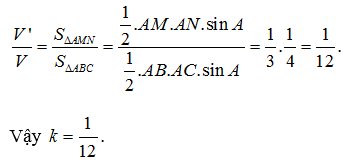Bạn đang xem: Công thức tính nhanh tỉ số thể tích khối đa diện – Toán Thầy Định Tại DongnaiArt

trong bài viết này sẽ tổng hợp các

công thức tính nhanh tỉ số thể tích của khối đa diện. kèm theo các ví dụ minh họa dễ hiểu. hãy tìm nó trong bài viết này! ιι

tôi. bài toán khối lượng bài toán khối lượng tam giác văn hóa vốn

Đây là bài giải bài tập 4 trang 25 SGK Hình học 12 (Cơ bản).

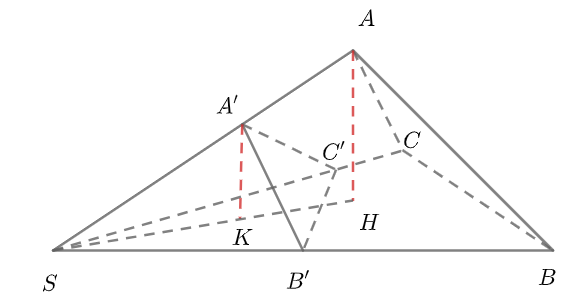
problem: (công thức 1) cho kim tự tháp s.abc. ba điểm a ‘, b’, c ‘lần lượt khác s được lấy trên các đường thẳng sa, sb, sc. chứng minh rằng

kiểm tra:

gọi h và k lần lượt là hình chiếu của a và a ‘lên mặt phẳng (sbc).

vì ah và a’k song song nên các điểm s, h, k, a, a ‘là đồng phẳng và ba điểm h, k, s nằm tại giao tuyến của hai mặt phẳng (sbc) và (tro) ). vì vậy h, k, s thẳng hàng.

chúng tôi có:

ii. công thức nhanh cho tỷ lệ thể tích

1. công thức nhanh cho tỷ lệ thể tích đỉnh

cũng như công thức trong mục i đã được kiểm tra. chúng tôi có các công thức sau:

công thức 2 :

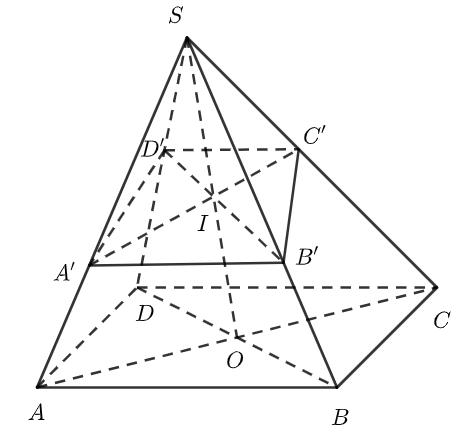
cho một hình chóp s.abcd có đáy abcd là một hình bình hành. trên các đoạn sa, sb, sc, sd lần lượt lấy các điểm a ‘, b’, c ‘, d’ khác với s sao cho a + c = b + d. ở đâu:

Xem Thêm : ✅ Công thức tính lim ⭐️⭐️⭐️⭐️⭐️

thì chúng ta có mối quan hệ về khối lượng

ví dụ 1:

cho một khối chóp s.abcd có đáy abcd là một hình bình hành và có thể tích bằng 77. mặt phẳng (α) đi qua một mặt cắt sc tại trung điểm n, cắt cạnh bên sb tại điểm m sao cho sm / sb = 6/7 và cắt cạnh sd tại điểm p. tính thể tích của hình chóp s.amnp.

giải pháp:

áp dụng công thức tính nhanh với a = 1, b = 7/6, c = 2 và d = a + c-b = 1 + 2-7 / 6 = 11/6 ta có:

công thức 3 : hai kim tự tháp có cùng chiều cao

Công thức này rất đơn giản và hiển nhiên, nhưng chúng ta thường thấy nó trong các bài toán. cụ thể, nếu hai hình chóp (h) và (h ‘) có hai đáy tương ứng là s và s’. đồng thời chúng có cùng độ cao h. thì chúng tôi có:

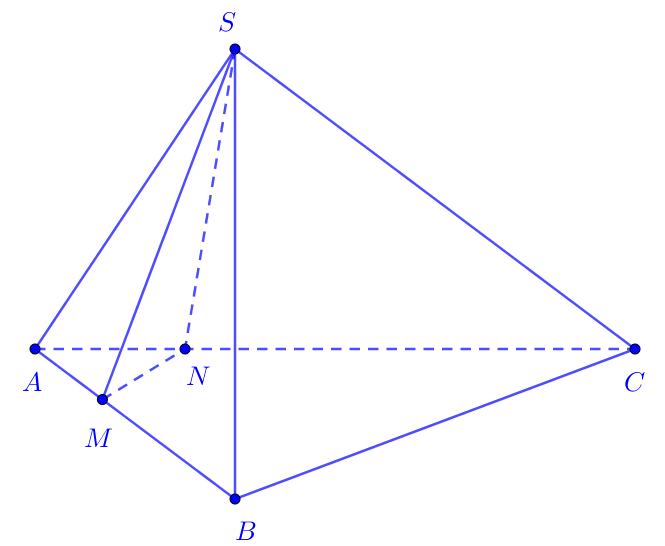
ví dụ 2:

cho kim tự tháp s.abc. điểm m nằm trên đoạn ab sao cho ab = 4h. điểm n nằm trong đoạn ac sao cho ac = 3an. Gọi v và v ‘lần lượt là thể tích của các hình chóp s.amn và s.abc. biết v ‘= kv. tìm k.

giải pháp:

hai khối hình chóp s.amn và s.abc có cùng mặt trên và mặt dưới nên chúng có cùng chiều cao.

do đó:

công thức 4: hai khối đa diện có cùng tỉ số k.

Xem Thêm : Cách viết thiệp sinh nhật Hay và Ý nghĩa dành tặng bạn bè, người thân

Hai khối đa diện (h) và (h ‘) được cho là có k tỷ số đồng dạng nếu có k tỷ số đồng dạng f biến (h) thành (h’). thì giả sử ab là một cạnh của (h) và f (ab) = a’b ‘nên a’b’ = kab. Gọi v và v ‘lần lượt là thể tích của (h) và (h’), khi đó ta có quan hệ thể tích sau:

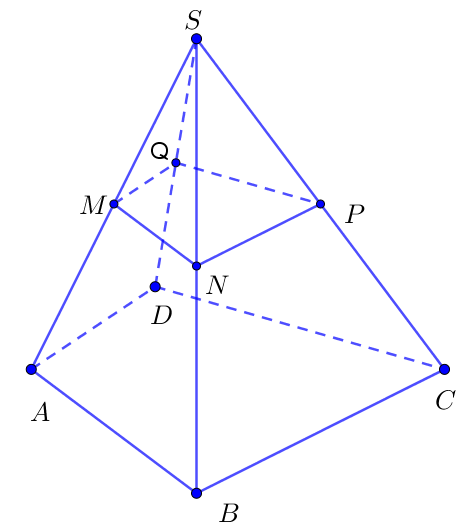
ví dụ 3:

cho khối kim tự tháp s.abcd. gọi m, n, p, q lần lượt là trung điểm của sa, sb, sc, sd. gọi v là thể tích của khối chóp s.mnpq. tính v biết rằng thể tích của hình chóp s.abcd là 12.

giải pháp:

Có thể dễ dàng nhận thấy rằng tỷ lệ vị từ vị tâm 2 chuyển đổi hình chóp s.mnpq thành s.abcd.

do đó:

2. công thức nhanh cho tỷ lệ thể tích lăng trụ

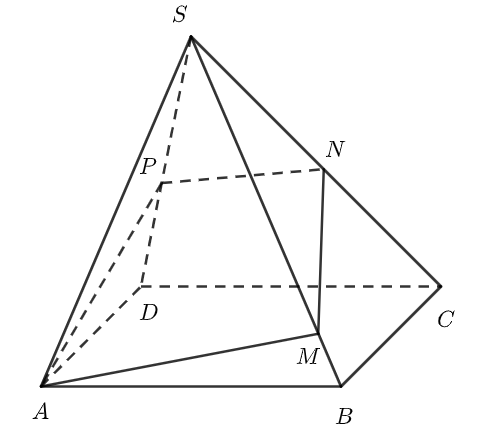
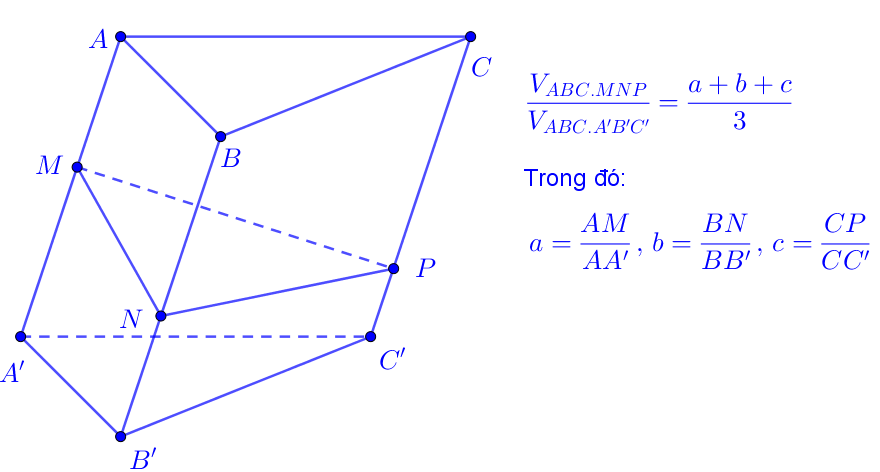
công thức 5: lăng trụ tam giác

cho lăng trụ tam giác abc.a’b’c ‘. trên các cạnh aa ‘, bb’, cc ‘lần lượt lấy các điểm m, n, p. thì chúng ta có mối quan hệ sau:

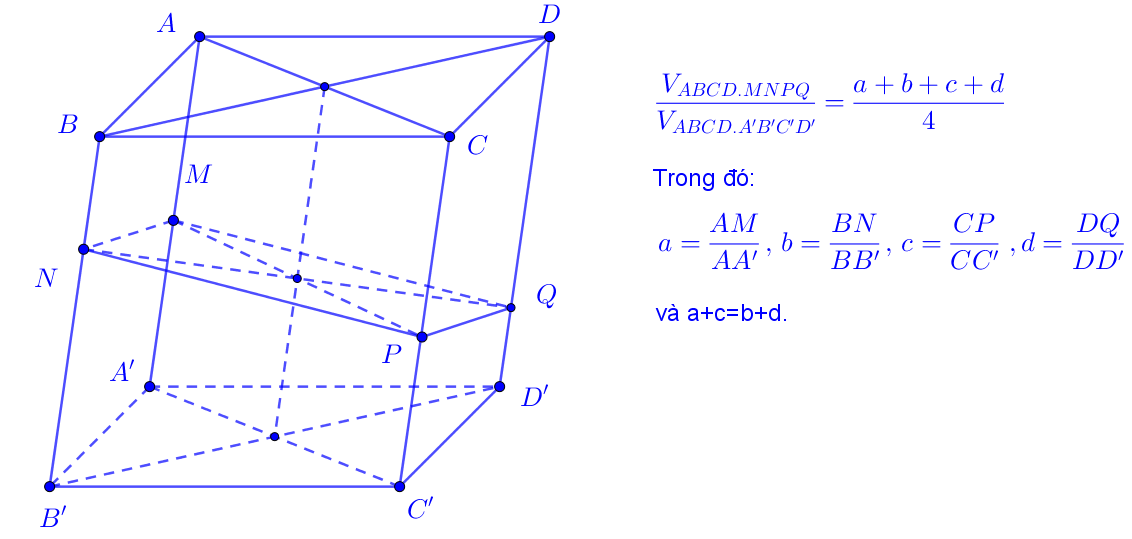
công thức 6: lăng trụ đứng là hình bình hành (hình hộp)

cho khối hộp abcd.a’b’c’d ‘. Trên các cạnh aa ‘, bb’, cc ‘, dd’ lần lượt lấy các điểm m, n, p, q sao cho m, n. p, q là đồng phẳng. thì chúng ta có mối quan hệ sau:

Trên đây là một số công thức liên quan đến tỉ lệ thể tích khối đa diện. luyện tập nhiều để sử dụng thành thạo. chúc bạn thành công!

xem thêm:

bát diện đều: công thức và bài tập về thể tích

• bát diện đều: công thức và bài tập về thể tích

  thể tích của khối tứ diện đều: khái niệm, công thức và bài tập chi tiết