Bạn đang xem: Những giải bài tập hình học 12 Tại DongnaiArt

Giải bài tập Hình học lớp 12 hay nhất | Giải bài tập Toán lớp 12

Giải bài tập Hình học lớp 12 hay nhất

Với giải bài tập Toán lớp 12 phần Hình học hay nhất được các Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách giáo khoa Hình học 12 giúp học sinh dễ dàng làm bài tập về nhà môn Toán lớp 12. Bên cạnh đó là các bài tóm tắt lý thuyết Toán lớp 12 [có kèm video bài giảng] và bộ bài tập trắc nghiệm theo bài học có lời giải chi tiết cùng với trên 100 dạng bài tập Toán lớp 12 với đầy đủ phương pháp giải giúp bạn ôn luyện để đạt điểm cao trong các bài thi môn Toán lớp 12.

Chương 1: Khối đa diện

• Toán lớp 12 Bài 1: Khái niệm về khối đa diện
• Toán lớp 12 Bài 2: Khối đa diện lồi và khối đa diện đều
• Toán lớp 12 Bài 3: Khái niệm về thể tích của khối đa diện
• Toán lớp 12 Ôn tập chương I
• Toán lớp 12 Câu hỏi trắc nghiệm chương I

Chương 2: Mặt nón, mặt trụ, mặt cầu

• Toán lớp 12 Bài 1 : Khái niệm về mặt tròn xoay
• Toán lớp 12 Bài 2 : Mặt cầu
• Toán lớp 12 Ôn tập chương 2 Hình học 12
• Toán lớp 12 Câu hỏi trắc nghiệm chương 2 Hình học 12

Chương 3: Phương pháp tọa độ trong không gian

• Toán lớp 12 Bài 1 : Hệ tọa độ trong không gian
• Toán lớp 12 Bài 2 : Phương trình mặt phẳng
• Toán lớp 12 Bài 3 : Phương trình đường thẳng trong không gian
• Toán lớp 12 Ôn tập chương 3 Hình học 12
• Toán lớp 12 Câu hỏi trắc nghiệm chương 3 Hình học 12
• Toán lớp 12 Ôn tập cuối năm Hình học 12

Tài liệu lý thuyết và các dạng bài tập Toán lớp 11:

• Các dạng bài tập Hình học lớp 12 chọn lọc
• 500 bài tập trắc nghiệm Hình học 12 có lời giải
• Tổng hợp lý thuyết Toán lớp 12 chi tiết

Giải bài tập Toán lớp 12 Bài 1: Khái niệm về khối đa diện

Trả lời câu hỏi Toán 12 Hình học Bài 1 trang 4: Nhắc lại định nghĩa hình lăng trụ và hình chóp.

Lời giải:

– Hình lăng trụ là hình gồm có hai đáy là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song, các mặt bên là hình bình hành, các cạnh bên song song hoặc bằng nhau

– Hình chóp là một hình không gian gồm có một đa giác gọi là mặt đáy, các tam giác chung đỉnh gọi là mặt bên, đỉnh chung của các mặt bên đó gọi là đỉnh của hình chóp.

Trả lời câu hỏi Toán 12 Hình học Bài 1 trang 6: Kể tên các mặt của hình lăng trụ ABCDE.A’B’C’D’E’ và hình chóp S.ABCDE (h.1.4 ).

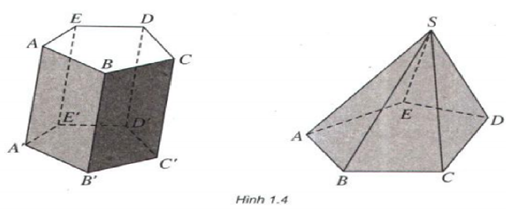
Lời giải:

– Các mặt của hình lăng trụ ABCDE.A’B’C’D’E’là: ABB’A’, BCC’B’, CDD’C’, DEE’D’, EAA’E’, ABCDE, A’B’C’D’E’

– Các mặt của hình chóp S.ABCDE là: SAB, SBC, SCD, SDE, SAE, ABCDE

Trả lời câu hỏi Toán 12 Hình học Bài 1 trang 8: Giải thích tại sao hình 1.8c không phải là một khối đa diện?

Lời giải:

Hình đa diện có tính chất: Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác

Nhưng hình 1.8c có cạnh AB là cạnh chung có 4 đa giác (không thỏa mãn t/c)

Trả lời câu hỏi Toán 12 Hình học Bài 1 trang 10: Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng hai lăng trụ ABD.A’B’D’ và BCD.B’C’D’ bằng nhau.

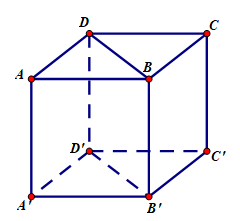
Lời giải:

Phép đối xứng qua mặt phẳng (BDD’B’) biến lăng trụ ABD.A’B’D’ thành BCD.B’C’D’

Xem Thêm : app chụp ảnh có con gấu trên mặt

⇒ hai lăng trụ ABD.A’B’D’ và BCD.B’C’D’ bằng nhau.

Bài 1 (trang 12 SGK Hình học 12): Chứng minh rằng một đa diện có các mặt là những tam giác thì tổng số các mặt của nó phải là một số chẵn. Cho ví dụ:

Lời giải:

* Gọi a là số cạnh, b là số mặt của khối đa diện.

Nếu khối đa diện có các mặt là tam giác thì mỗi mặt có ba cạnh. Trong ba cạnh đó mỗi cạnh lần lượt là cạnh chung của hai mặt.

Ta có 3b = 2a. Nghĩa là b chẵn.

Mà 2a chia hết cho 2 nên 3b cũng chia hết cho 2

⇒ b chia hết cho 2 hay b là số chẵn.

* Ví dụ: hình tứ diện đều có 4 mặt

………………………………

………………………………

………………………………

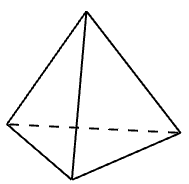
Giải bài tập Toán lớp 12 Bài 2: Khối đa diện lồi và khối đa diện đều

Trả lời câu hỏi Toán 12 Hình học Bài 2 trang 15: Tìm ví dụ về khối đa diện lồi và khối đa diện không lồi trong thực tế.

Lời giải:

Khối đa diện lồi trong thực tế: kim tự tháp Ai Cập, viên kim cương, rubic

Khối đa diện không lồi trong thực tế: cái bàn

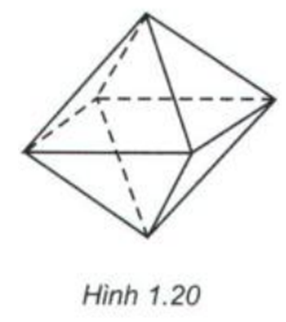
Trả lời câu hỏi Toán 12 Hình học Bài 2 trang 16: Đếm số đỉnh, số cạnh của khối bát diện đều.

Lời giải:

Khối bát diện đều có 6 đỉnh và 12 cạnh

Trả lời câu hỏi Toán 12 Hình học Bài 2 trang 17: Chứng minh rằng tam giác IEF, IFM, IMN, INE, JEF, JFM, JMN và JNE là những tam giác đều cạnh bằng a/2.

Xem Thêm : Báo giá chụp hình cho bé

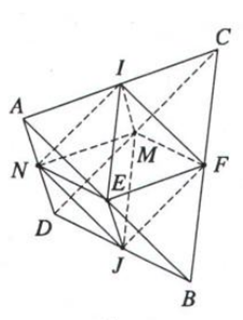
Lời giải:

ABCD là tứ diện đều ⇒ tam giác ABC đều ⇒ AB = BC = CA = a

I, E, F lần lượt là trung điểm của các cạnh AC, AB, BC nên ta có IE, IF, EF là các đường trung bình của tam giác ABC

⇒ IE = 1/2 BC = 1/2 a

IF = 1/2 AB = 1/2 a

EF = 1/2 AC = 1/2 a

Nên tam giác IEF là tam giác đều cạnh bằng a/2

Chứng minh tương tự ta có: IFM, IMN, INE, JEF, JFM, JMN và JNE là những tam giác đều cạnh bằng a/2

Trả lời câu hỏi Toán 12 Hình học Bài 2 trang 18: Chứng minh rằng AB’CD’.A’B’C’D’ có cạnh bằng a (h.1.22b).

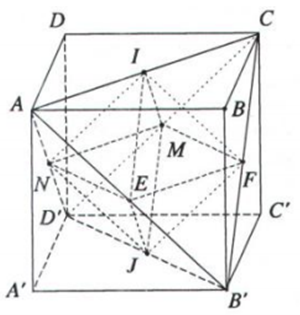
Lời giải:

ABCD.A’B’C’D’ là hình lập phương cạnh a nên các mặt là các hình vuông cạnh a

Tứ diện AB’CD’ có các cạnh là các đường chéo của các mặt bên hình lập phương ABCD.A’B’C’D’ nên tứ diện AB’CD’ có các cạnh bằng nhau ⇒ AB’CD’ là tứ diện đều

Cạnh của tứ diện đều AB’CD’ bằng độ dài đường chéo của hình vuông cạnh a và bằng a√2

Bài 1 (trang 18 SGK Hình học 12): Cắt bìa theo mẫu dưới đây (h.123), gấp theo đường kẻ, rồi dán các mép lại để được các hình tứ diện đều, hình lập phương và hình bát diện đều.

Lời giải:

………………………………

………………………………

………………………………

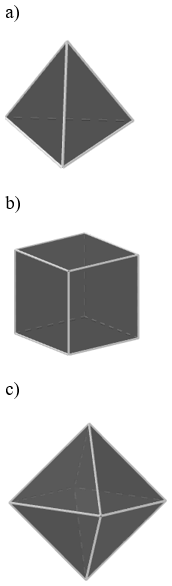
Ngân hàng trắc nghiệm miễn phí ôn thi THPT Quốc Gia tại dongnaiart.edu.vn

• Hơn 75.000 câu trắc nghiệm Toán có đáp án
• Hơn 50.000 câu trắc nghiệm Hóa có đáp án chi tiết
• Gần 40.000 câu trắc nghiệm Vật lý có đáp án
• Hơn 50.000 câu trắc nghiệm Tiếng Anh có đáp án
• Kho trắc nghiệm các môn khác