Bạn đang xem: Định nghĩa đường trung tuyến trong tam giác và một số dạng toán thường gặp Tại DongnaiArt

Đường trung tuyến trong tam giác là một trong những kiến thức cơ bản yêu cầu học sinh phải nắm vững để có thể áp dụng vào bài tập và những bài kiểm tra. Nếu như các bạn có lỡ quên thì cũng đừng lo lắng nhé, vì bài viết này sẽ giúp các bạn ôn lại những kiến thức tổng quát về đường trung tuyến và những dạng toán thường gặp của đường trung tuyến. Cùng tìm hiểu ngay nhé

Định nghĩa đường trung tuyến trong tam giác

Đường trung tuyến là một đường thẳng đi qua trung điểm của đường thẳng đó. Trung điểm là điểm chia đoạn thẳng thành hai phần bằng nhau.

Bạn đang xem: định nghĩa đường trung tuyến

Đường trung tuyến trong tam giác là đoạn thẳng nối từ đỉnh đến trung điểm của cạnh đối diện và một tam giác có 3 đường trung tuyến

Công thức tính đường trung tuyến:

Cho a, b, c lần lượt là độ dài 3 cạnh của tam giác, độ dài 3 đường trung tuyến ta có thể tính bằng cách áp dụng định lý Apollonius như sau:

ma=2b2+2c2-a22mb=2a2+2c2-b22mc=2a2+2b2-c22

Tính chất đường trung tuyến trong tam giác

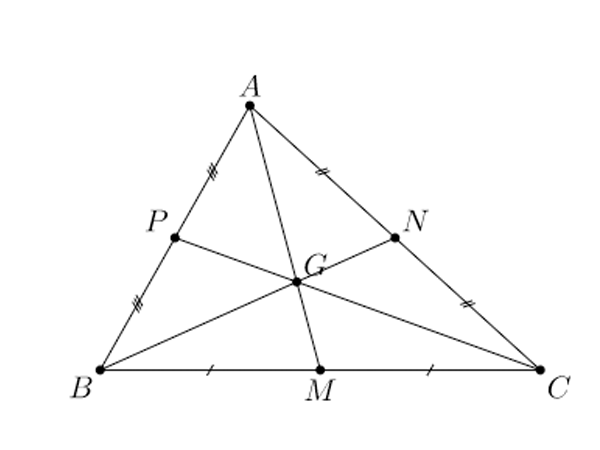
Đường trung tuyến trong tam giác (Nguồn: Internet)

• Ba đường trung tuyến của một tam giác cùng đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác.

• Khoảng cách từ trọng tâm đến mỗi đỉnh của tam giác bằng ⅔ đường trung tuyến tương ứng với đỉnh đó.

• Khoảng cách từ trọng tâm đến trung điểm của mỗi cạnh bằng ⅓ đường trung tuyến tương ứng với điểm đó.

• Đối với tam giác đều đường thẳng đi qua một đỉnh bất kỳ và đi qua trọng tâm của tam giác sẽ chia tam giác đó thành hai tam giác có diện tích bằng nhau.

• Đặc biệt 3 đường trung tuyến của 1 tam giác đều sẽ chia tam giác đó thành 6 tam giác có diện tích bằng nhau.

• Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng ½ cạnh huyền.

Các dạng toán thường gặp về đường trung tuyến

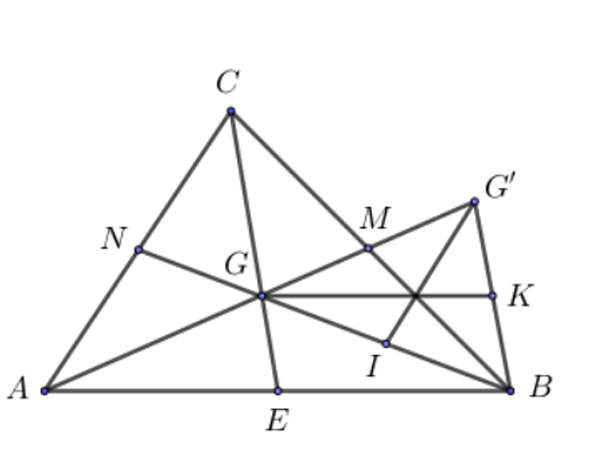
Bài tập 1: Cho tam giác ABC với G là trọng tâm. Trên cạnh AG lấy điểm G’ sao cho G là trung điểm của đoạn AG’. Yêu cầu so sánh:

1. Những cạnh của tam giác BGG’ với các đường trung tuyến của tam giác ABC.
2. Những đường trung tuyến của tam giác BGG’ với các cạnh của tam giác ABC.

Hình minh họa (Nguồn: Internet)

Bài giải:

1. Ta có BG cắt AC tại điểm N, CG cắt AB tại điểm E và G là trọng tâm của tam giác ABC.

Tham khảo: Pascal

Xem Thêm : 10 quốc gia không giáp biển vẫn có lực lượng hải quân – Infonet

=> GA = ⅔ AM

Vì G là trung điểm của AG’ => GA =GG’

Suy ra: GG’ = ⅔ AM

Theo giả thuyết ta có G là trọng tâm của tam giác ABC

=> GB = ⅔ BN

Mặt khác: GM = ½ AG (vì G là trọng tâm)

AG = GG’ => GM = ½ GG’

M là trung điểm của đoạn GG’

Vì GM = MG’ và MB = Mc => tam giác GMC = tam giác G’MB

Suy ra: BG’ = CG

Mà CG = ⅔ CE (G là trọng tâm của tam giác ABC)

=> BG’ = ⅔ CE

Vậy mỗi cạnh của tam giác BGG’ bằng ⅔ các đường trung tuyến của tam giác ABC.

1. Ta có BM là đường trung tuyến của tam giác BGG’

mà điểm M lại là trung điểm của đoạn BC nên BM = ½ BC

I là trung điểm của BG => IG = ½ BG

G là trọng tâm tam giác ABC => GN = ½ BG

Suy ra: IG = GN

=> tam giác IGG’ = tam giác NGA theo trường hợp cạnh.góc.cạnh

=>IG’ = AN =>IG’ = ½ AC

Xem thêm: woody allen phim

Xem Thêm : máy bơm nước hãng nào tốt nhất

Gọi K là trung điểm của đoạn BG => GK là trung tuyến của tam giác BGG’

Mặt khác, vì G là trọng tâm của tam giác ABC => GE = ½ GC

Mà K là trung điểm của BG’ => KG” = EG

Vì tam giác GMC = tam giác G’BM (chứng minh trên)

=> tam giác GCM = tam giác G’BM theo trường hợp góc so le trong

=>CE//BG => tam giác AGE = tam giác AG’B theo trường hợp đồng vị

Do đó tam giác AGE = tam giác GG’K (c.g.c) => AE = GK

Mà AE = ½ AB nên GK = ½ AB

Vậy mỗi đường trung tuyến của tam giác BGG’ bằng ½ các cạnh của tam giác ABC.

Bài tập 2: Cho tam giác ABC có 2 đường đường trung truyến AA’ và BB’ cắt nhau tại điểm O. Yêu cầu: Tính diện tích tam giác ABC, biết diện tích tam giác AOB bằng 5(đvdt)

Hình minh họa (Nguồn: Internet)

Bài giải:

Ta có:

S(AOB) = ⅔ S(AA’B) (vì AO = ⅔ AA’)

S(ABA’) = ½ S(ABC) (vì BA’ = ½ BC)

Từ đó suy ra: S(ABC) = 2S(ABA’) = 3S(AOB)

Theo đề bài ta có: S(AOB) = 5(đvdt) => S(ABC) = 3.5 =15(đvdt).

Bên trên là kiến thức tổng quát về đường trung tuyến trong tam giác và một số dạng toán liên quan. Hy vọng bài viết có thể giúp ích cho các bạn trong quá trình học tập.

Tham khảo: Cách lấy lại mật khẩu thanh toán Zalo Pay khi bị quên nhanh, đơn giản