Cùng xem Bài 52,53,54 ,55,56,57 trang 79,80 Toán 7 tập 2 – Dethikiemtra.com trên youtube.

Tính chất ba đường trung trực của một tam giác: Giải bài 52 tr.79;

Sau 52.Chứng minh định lý: Nếu Δ có đường trung trực đồng thời là đường trung trực của một cạnh thì Δ cân.

Hướng dẫn: Hãy coi Δabc và ah là các đường trung tuyến, đồng thời là các đường thẳng đứng

a bc va hb = hc

Xét hai hình vuông hab và hac:

hb = hc;∠h1 = h2 = 900

À: mặt chung

Vậy Δhab = Δhac => ab = ac

Vậy abc nằm trong

bài 53.Ba gia đình quyết định cùng nhau đào giếng. Nên chọn vị trí đặt giếng ở đâu để khoảng cách từ giếng đến nhà đều nhau?

Giải thích: Do điểm đào giếng nằm ngoài ba ngôi nhà (ba ngôi nhà không nằm trên một đường thẳng) nên điểm này là giao điểm của ba đường trung trực-trực tâm của ba cạnh trong Δ và ba các đỉnh của ngôi nhà.

Bài 54, trang 80. Vẽ đường tròn đi qua ba đỉnh của tam giác abc khi:

a) a, b, c đều nhọn

b) a = 900

c)∠a> 900

Giải thích: Đường tròn đi qua ba đỉnh của Δ được gọi là đường tròn ngoại tiếp Δ này. Để vẽ đường tròn ngoại tiếp ta cần xác định tâm đường tròn. Để xác định tâm ta vẽ giao điểm của hai đường trực tâm và hai đường trung trực (cũng là ba giao điểm cần tìm)

Nhận xét:

Xem Thêm : Bài 9 trang 70 SGK Toán 9 Tập 2 – VietJack.com

– Nếu có ba góc nhọn thì tâm đường tròn ngoại tiếp là Δ.

– Nếu Δ là góc vuông thì tâm đường tròn nằm trên cạnh huyền (tâm đường tròn là trung điểm của cạnh huyền)

– Nếu góc tù thì tâm đường tròn ngoại tiếp tam giác.

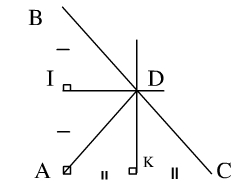
bài 55.Chế độ xem bên:

Chứng minh ba điểm b, c, d thẳng hàng

Gợi ý: chứng minh rằng adb + adc = 1800

Hướng dẫn giải Bài 55:

Từ hình vẽ ta có:

dk là trực giao của ac, và di là trực giao của ab. Vậy Δadk = Δcdk (c.c.c)

=>adk = cdk

Hay dk là tia phân giác adc

=> ∠adk = 1/2 adc

Δadi = Δbdi (c.c.c)

=>adi = bdi

=>di là tia phân giác của adb

=>adi = 1/2 adb

Vì ac // di (vuông góc với ab) nên dk ac

=>Dickie

Xem Thêm : Câu chuyện về Chim Én và Dế Mèn – THPT Thăng Long

hoặc adk + adi = 90º

Vậy 1/2 adc + 1/2 adb = 900

=>adc + adb = 1800

=> ∠bdc = 180º => ∠bdc là góc bẹt nên ba điểm b, c, d thẳng hàng.

Đã xuất bản 56 trang 80. Vận dụng bài tập 55 để chứng minh điểm cách đều ba đỉnh của hình vuông là trung điểm của cạnh huyền của hình vuông.

Từ đó, tính độ dài đường trung tuyến kẻ từ đỉnh của góc vuông đến độ dài cạnh huyền của hình vuông Δ.

Giải thích: a) Giả sử Δabc thẳng đứng tại a. Vẽ đường trung trực của hai cạnh ab và ac cắt nhau tại m. Ta chứng minh m là trung điểm của bc.

Vì m là giao điểm của hai đường thẳng d1, d2

ab, ac thì ab ⊥ ac nên b, m, c thẳng hàng (Bài 55)

Vì ma = mb (m thuộc tiệm cận đứng của ab)

ma = mc (m nằm trên đường thẳng đứng của ac)

=>mb = mc

Vì b, m, c thẳng hàng và m cách đều bc nên m là trung điểm của bc

b) m là trung điểm của bc =>;mb = 1/2 BC

Vậy am = mb nên ma = 1/2 bc

Vậy độ dài từ đỉnh đến đường trung tuyến bằng một nửa độ dài cạnh huyền.

Bài 57 Toán 7. Có một chi tiết máy bị hỏng (viền ngoài là hình tròn). Cách xác định bán kính của đường viền này.

Lấy ba điểm a, b, c khác nhau trên đường bao ngoài và suy ra đường tròn ngoại tiếp là Δabc của đường bao ngoài. Vậy tâm đường tròn ngoại tiếp là giao điểm của hai đường trung trực của hai cạnh ab và ac nên bán kính là độ dài đoạn thẳng kẻ từ giao điểm o đến a.

Nguồn: https://dongnaiart.edu.vn
Danh mục: Tin tức

Lời kết: Trên đây là bài viết Bài 52,53,54 ,55,56,57 trang 79,80 Toán 7 tập 2 – Dethikiemtra.com. Hy vọng với bài viết này bạn có thể giúp ích cho bạn trong cuộc sống, hãy cùng đọc và theo dõi những bài viết hay của chúng tôi hàng ngày trên website: Dongnaiart.edu.vn