Bạn đang xem: Luyện tập: Giải bài 17 18 19 trang 51 52 sgk Toán 9 tập 1 Tại DongnaiArt

Bài tập 3. Đồ Thị Hàm Số \(y = ax + b (a ≠ 0)\), Chương 2 – Hàm Số Bậc Nhất, SGK Toán 9 Tập 1. Bài 17 18 19 trang 51 52 sgk toán 9 tập 1 bao gồm tổng hợp các công thức, lý thuyết và các phương pháp giải trong phần đại số trong SGK toán 9 giúp học sinh học tốt môn Toán lớp 9.

Lý thuyết

1. Đồ thị hàm số $y = ax + b (a 0)$

Đồ thị của hàm số\(y = ax + b (a \neq 0)\) là một đường thẳng:

– Cắt trục tung tại một điểm có tọa độ bằng b

– Song song với đường thẳng \(y = ax\) nếu \(b \neq 0\); trùng với đường thẳng y=ax nếu b=0

Lưu ý: Đồ thị của hàm số \(y = ax + b (a \neq 0)\) còn gọi là đường thẳng\(y = ax + b\); b gọi là gốc tọa độ của đường thẳng

2. Cách vẽ đồ thị của hàm $y = ax + b (a 0)$

Vẽ đường thẳng đi qua hai điểm \(p(0;b)\) và \(q(\frac{-b}{a};0)\) ta được số đồ thị của hàm\ (y = ax + b\)

Dưới đây là hướng dẫn giải bài 17, 18, 19 trang 51, 52 tập 1 SGK Toán 9. Các em đọc kỹ câu hỏi trước khi giải bài nhé!

Bài tập

giaibaisgk.com giới thiệu đến các bạn lời giải đầy đủ và chi tiết các bài tập Đại số 9 Chương 17, 18, 19 trang 51, 52 SGK Toán 9, Bài 1 §3 SGK Toán. Đồ thị của hàm số \(y = ax + b (a ≠ 0)\) trong chương thứ hai—hàm số bậc nhất dành cho bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:

1. Giải bài 17 trang 51 sgk toán 9 tập 1

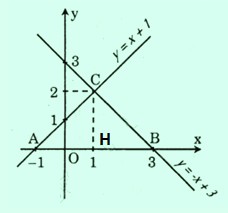
a) Vẽ các hàm $y = x + 1$ và $y = -x + 3$ trên cùng một mặt phẳng tọa độ.

b) Hai đường thẳng $y = x + 1$ và $y = -x + 3$ cắt nhau tại $c$ và cắt các trục $ox$ tại $a$ và $b$ tương ứng. Tìm tọa độ của điểm $a, b, c.$. $

c) Tính chu vi và diện tích tam giác $abc$ (số đo các trục tính bằng xăng-ti-mét).

Giải pháp:

a) Để vẽ đồ thị hàm số:

+) hàm\(y=x+1\):

Cho \(x=0 \rightarrow y=0+1=1 \rightarrow (0; 1)\)

Đối với \(y=0 \rightarrow 0=x+1 \rightarrow x=-1 \rightarrow (-1; 0)\)

Đồ thị hàm số \(y=x+1\) là đường thẳng đi qua hai điểm \((-1; 0)\) và \((0;1)\ ).

+) hàm\(y=-x+3\)

Cho \(x=0 \rightarrow y=0+3 =3 \rightarrow (0; 3)\)

Cho \(y=0 \rightarrow 0=-x+3 \rightarrow x=3 \rightarrow (3; 0)\)

Đồ thị của hàm số \(y=-x+3\) là đường thẳng đi qua hai điểm \((3; 0)\) và \((0; 3)\ ).

Ta có hình sau:

b) +) \(c\) là giao điểm của \(y=x+1\) và \(y=-x+3\) nên Tọa độ của (c\) là nghiệm của phương trình:

\(x+1=-x+3\) \(\leftrightarrow x+x=3-1\)

\(\leftrightarrow 2x=2\) \(\leftrightarrow x=1\).

Tọa độ của \(c\) là: \(y=1+1=2\).

Vậy \(c(1; 2)\).

+) \(a\) là giao điểm của \(y=x+1\) và trục hoành \(ox: y=0\) nên \(a ) ) là:

\(x+1=0\)

\(\leftrightarrow x=-1\)

Vậy \(a(-1; 0) \).

Xem Thêm : Mẫu biên bản hội nghị cán bộ công chức mới nhất 2023

+) \(b\) là giao điểm của \(y=-x+3\) và trục hoành \(ox: y=0\), nên tọa độ của điểm ( b \ ) là:

\(-x+3=0\)

\(\leftrightarrow -x+3=0\) \(\leftrightarrow x=3\)

Vậy \( b(3; 0)\)

c) Ta có: \(ab=4,\)

+) Áp dụng định lý Pitago, ta dễ dàng tính được:

\(ac=\sqrt{2^2+2^2}=\sqrt{4+4}=\sqrt 8 =2\sqrt 2\)

\(bc=\sqrt{2^2+2^2}=\sqrt{4+4}=\sqrt 8 =2\sqrt 2\)

Vậy chu vi của tam giác \(abc\) là:

\(ab+bc+ac=4+2\sqrt{2}+2\sqrt{2}=4+4\sqrt{2}(cm)\)

+) Chiều cao của tam giác \(abc\) là: ch = \(2\).

+) Diện tích của tam giác \(abc\) là:

\(s=\dfrac{1}{2}.ab.ch=\dfrac{1}{2}.4.2=4(cm^2)\)

2. Giải bài 18 trang 52 SGK Toán 9 Tập 1

a) Biết rằng với $x = 4$, hàm $y = 3x + b$ ước tính là $11$. Tìm $b$. Vẽ đồ thị của hàm với giá trị $b$ vừa tìm được.

b) Biết rằng đồ thị của hàm số $y = ax + 5$ đi qua điểm $a(-1;3)$. find $a.$ vẽ hàm với giá trị $a$ vừa tìm được.

Giải pháp:

a) Thay \(x = 4\) và \(y = 11\) bằng \(y = 3x +b\), ta được:

\(11 = 3,4 + b\)

\(\leftrightarrow 11=12+b\)

\(\leftrightarrow 11-12 =b\)

\(\leftrightarrow b=-1\).

Hàm số đã cho trở thành: \(y = 3x – 1\).

+ cho \(x=0 \rightarrow y=3.0 – 1=-1 \rightarrow a(0; -1)\)

Đối với \( y=0 \rightarrow 0=3.x – 1 \rightarrow x=\dfrac{1}{3} \rightarrow b{\left(\dfrac{1}{ 3}; 0 \phải)}\)

Vậy đồ thị của hàm số \(y=3x+b\) là đường thẳng \(2\) điểm \(a(0;-1)\) và \( b \ left({\dfrac{1}{3};0}\right)\). Ta có đồ thị sau:

b) Thay \(x= -1\) rồi \(y=3\) thay công thức hàm \(y=ax+5\), chúng tôi nhận được:

\( 3= a.(-1) + 5 \)

\(\leftrightarrow 3 = -a +5\)

\(\leftrightarrow a = 5-3\)

\(\leftrightarrow a = 2\)

Hàm số đã cho trở thành: \(y = 2x + 5\).

+ cho \(x = 0 \rightarrow y = 2.0 +5=5 \rightarrow a(0; 5)\)

Cho \(y=0 \rightarrow 0= 2. x +5 \rightarrow x=\dfrac{-5}{2} \rightarrow b {\left(-\dfrac{5 }{2}; 0 \phải)}\)

Xem Thêm : Top 15 Bài văn thuyết minh về cây tre hay nhất – Toplist.vn

Vậy đồ thị của hàm số là đường thẳng đi qua hai điểm \(a(0; 5)\) và \(b \left( { – \dfrac{5}{2} ;0 } \ Phải)\).

3. Giải bài 19 trang 52 SGK Toán 9 tập 1

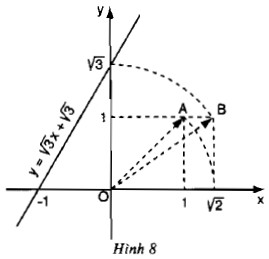
Đồ thị của hàm số $y = \sqrt{3}x + \sqrt{3}$ được vẽ bằng compa và thước kẻ (h.8)

Tìm hiểu cách vẽ nó, sau đó lặp lại các bước.

Ứng tuyển. Viết hàm số y = $\sqrt{5}$x + $\sqrt{5}$ bằng compa và thước kẻ.

Hướng dẫn. Tìm điểm trên trục tung có tọa độ $\sqrt{5}$.

Giải pháp:

+ Chức năng vẽ: \(y=\sqrt 3 x + \sqrt 3\)

Đối với \(x= 0 \rightarrow y = \sqrt 3 . 0 + \sqrt 3 = \sqrt 3 \rightarrow m(0; \sqrt 3)\).

Đối với \(y=0 \rightarrow 0 = \sqrt 3 . x + \sqrt 3 \rightarrow x= -1 \rightarrow n(-1; 0)\).

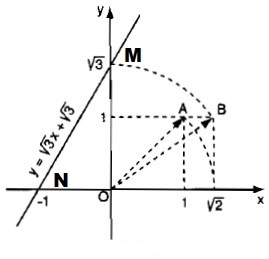
Đồ thị hàm số \(y=\sqrt 3 x + \sqrt 3\) là đường thẳng đi qua hai điểm \(m(0; \sqrt 3)\) và \ ( n (- 1; 0)\)

+ Hãy xác định vị trí của điểm \(m(0; \sqrt 3)\) trên trục tung:

Bước \(1\): Xác định điểm \(a(1; 1)\) trên mặt phẳng tọa độ \(oxy\). Khi đó theo định lý Pitago, ta có:

\(oa^2=1^2+1^2=2 \leftrightarrow oa =\sqrt 2\)

bước \(2\): Dùng compa vẽ tâm cung tròn \(o\) bán kính\(oa =\sqrt 2\). Cung này cắt trục \(ox\) tại vị trí \(c\) thì tọa độ của \(c\) là \(\sqrt 2\).

Bước \(3\): Xác định điểm \(b( \sqrt 2; 1)\). Khi đó theo định lý Pitago, ta có:

\(ob^2=(\sqrt 2)^2+1^2=2=1=3 \leftrightarrow ob =\sqrt 3\)

bước \(4\): Vẽ một cung tròn bằng compa, tâm của hình tròn là \(o\), và bán kính là \(ob=\sqrt 3\). Sau đó cung này cắt trục tung tại vị trí \(\sqrt 3\). Ta có thể xác định điểm \(m(0; \sqrt 3)\).

Bước\(5\): vẽ đường thẳng đi qua hai điểm \(m\) và \(n\) ta được đồ thị hàm số \(y=\sqrt 3 x + sqrt 3\).

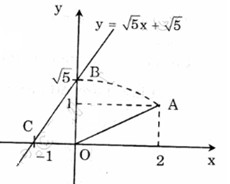
+ Ứng dụng: hàm vẽ đồ thị \(y = \sqrt 5 x + \sqrt 5 \)

Cho \(x= 0 \rightarrow y = \sqrt 5 . 0 + \sqrt 5 = \sqrt 5 \rightarrow b(0; \sqrt 5)\).

Cho \(x= -1 \rightarrow y = \sqrt 5 . (-1) + \sqrt 5 = 0 \rightarrow c(-1; 0)\).

Bước \(1\): Xác định điểm \(a(2; 1)\) trên mặt phẳng tọa độ \(oxy\).

Vận dụng định lý Pitago, ta có:

\(oa^2=2^2+1^2=4+1=5 \leftrightarrow oa = \sqrt 5\)

Bước\(2\): Vẽ một cung có tâm \(o\) làm bán kính \(oa=\sqrt 5\). Cung này cắt trục \(oy\) tại điểm \(b\) tại tọa độ \(\sqrt 5\). Chúng ta có thể xác định điểm \(b\).

bước \(3\): Vẽ đường thẳng đi qua hai điểm \(b(0; \sqrt 5)\) và \(c(-1; 0)\) ta được đồ thị Hàm \(y = \sqrt 5 x + \sqrt 5 \).

Trước:

• Giải bài 15 16 trang 51 SGK Toán 9 Tập 1

Tiếp theo:

• Giải bài 20 21 22 trang 54 55 SGK Toán 9 Tập 1

Xem thêm:

• Câu hỏi khác 9
• Học tốt vật lý lớp 9
• Học tốt môn sinh học lớp 9
• Học tốt ngữ văn lớp 9
• Điểm tốt môn lịch sử lớp 9
• Học tốt môn địa lý lớp 9
• Học tốt tiếng Anh lớp 9
• Tiếng Anh lớp 9 thí điểm
• Học Khoa học Máy tính Lớp 9
• Học tốt GDCD lớp 9

Chúc các em tham khảo và giải bài tập 17 18 19 SGK toán 9 trang 51 52 sgk toán 9 tập 1 thành công!

“Môn thể thao nào đã khó giabaisgk.com”